Question

18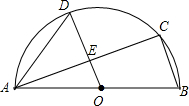．如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．
（1）若∠B=80°，求∠CAD的度数；
（2）若AB=8，AC=6，求DE的长．

Answer 1

分析 （1）根据平行线的性质求出∠AOD，根据等腰三角形的性质求出∠OAD，根据圆周角定理求出∠CAB，计算即可；
（2）根据勾股定理求出BC，根据三角形中位线定理求出OE，结合图形计算．

解答 解：（1）∵OD∥BC，
∴∠AOD=∠B=80°，
∴∠OAD=∠ODA=50°，
∵AB是半圆O的直径，
∴∠C=90°，
∴∠CAB=10°，
∴∠CAD=50°-10°=40°；
（2）∵∠C=90°，AB=8，AC=6，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{7}$，
∵OD∥BC，OA=OB，
∴OE=$\frac{1}{2}$BC=$\sqrt{7}$，
∴DE=4-$\sqrt{7}$．

点评 本题考查的是圆周角定理、三角形中位线定理的应用，掌握直径所对的圆周角是直角、灵活运用勾股定理是解题的关键．