题目内容
9．若|a-12|+（3a-b-k）2=0，且b＜0，试确定k的取值范围．分析 根据偶次方，绝对值的非负性得出a-12=0，3a-b-k=0，求出a和b的值，得出关于k的不等式，求出不等式的解即可．
解答 解：∵|a-12|+（3a-b-k）2=0，
∴a-12=0，3a-b-k=0，
∴a=12，
∴代入得：36-b-k=0，
∴b=36-k，
∵b＜0，
∴36-k＜0，
∴k＞36，
即k的取值范围是k＞36．
点评 本题考查了解一元一次不等式，解一元一次方程，绝对值的非负性，偶次方的非负性的应用，解此题的关键是得出关于k的不等式，难度适中．
练习册系列答案
相关题目
19．
如图，分别以点A，B为圆心作圆，使两圆都经过线段AB上一点F，这两圆的位置关系是（ ）
如图，分别以点A，B为圆心作圆，使两圆都经过线段AB上一点F，这两圆的位置关系是（ ）| A． | 相交 | B． | 内切 | C． | 外切 | D． | 外离 |
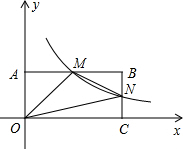如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（6，3），直线y=-$\frac{1}{2}$x+4交AB，BC分别于点M，N，反比例函数y=$\frac{k}{x}$的图象经过点M，N．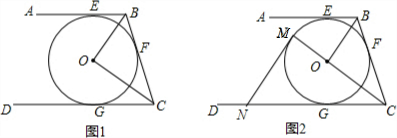
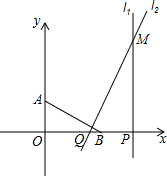如图，点A（0，2）、B（4，0），点P从（8，0）出发，以每秒2个单位长度沿x轴向坐标原点O匀速运动，同时，点Q从B点出发，以每秒1个单位长度沿x轴向坐标原点O匀速运动，过点P作x轴的垂线l，过点Q作AB的垂线l2，它们的交点为M．设运动的时间为t（0＜t＜4）秒
18．
解集在数轴上表示为如图所示的不等式组的是（ ）
解集在数轴上表示为如图所示的不等式组的是（ ）| A． | $\left\{\begin{array}{l}{x＞-1}\\{x≥3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x＜3}\\{x≤-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x＜3}\\{x≥-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x＞3}\\{x≤-1}\end{array}\right.$ |