题目内容
如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.
(1)求证:AB∥DE;
(2)求EG的长.
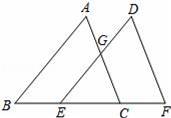

【考点】全等三角形的判定与性质.
【专题】计算题.
【分析】(1)由BE=CF,利用等式的性质得到BC=EF,利用SSS得到三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证;
(2)由BE=CE得到E为BC中点,再由GE与AB平行,利用平行线等分线段定理得到G为AC中点,即GE为中位线,利用中位线定理得到AB=2EG,即可求出EG的长.
【解答】解:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,

 ,
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE;
(2)∵GE∥AB,E为BC中点,
∴G为AC中点,即GE为△ABC中位线,
∴EG=
 AB=5.
AB=5.
【点评】此题考查了全等三角形的判定与性质,以及平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,那么x的值是( )
,那么x的值是( ) B.
B. C.
C. D.
D.
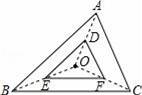

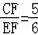
 ,CD=4,求BD的长.
,CD=4,求BD的长.




 B.
B.
 C.
C.
 D.
D.