题目内容
如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（ ）
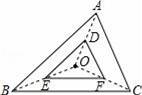
A．1：6 B．1：5 C．1：4 D．1：2
C【考点】位似变换．
【专题】计算题．
【分析】根据两三角形为位似图形，且点O是位似中心，D、E、F分别是OA、OB、OC的中点，求出两三角形的位似比，根据面积之比等于位似比的平方即可求出面积之比．
【解答】解：∵△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，
∴两图形的位似之比为1：2，
则△DEF与△ABC的面积比是1：4．
故选C．
【点评】此题考查了位似变换，位似是相似的特殊形式，位似比等于相似比，其对应的面积比等于相似比的平方．
练习册系列答案
相关题目
m，圆心角为120°，则此扇形的弧长是 cm．
|+2cos30°+（9﹣
）0+
．
= ．
；若由甲队先做10天，剩下的工程再由甲、乙两队合作30天完成．