题目内容
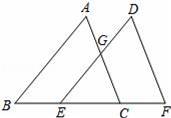
在△ABC中,∠ACB=90°.经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
(1)若∠ABC=45°,CD=1(如图),则AE的长为 ;
(2)写出线段AE、CD之间的数量关系,并加以证明;
(3)若直线CE、AB交于点F,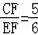
 ,CD=4,求BD的长.
,CD=4,求BD的长.


【考点】相似形综合题.
【分析】(1)首先在直角三角形CDB中利用CD求得BC,然后在直角三角形ABC中求得AE即可;
(2)根据上题得到的结论猜想两条线段之间具有二倍关系,证得△GCD∽△GAE后即可证明猜想正确.
(3)分当点F在线段AB上时和点F在线段BA的延长线上时利用△AGH∽△AEB求得线段BD的长即可.
【解答】(1)解:
∵∠ABC=45°,
∴∠CBD=45°,
∵CD=1,
∴BC=
 ,
,
∵∠ACB=90°,∠ABC=45°,
AE=2.
(2)线段AE、CD之间的数量关系为AE=2CD.
证明:如图1,延长AC与直线l交于点G.
依题意,可得∠1=∠2.
∵∠ACB=90°,
∴∠3=∠4.
∴BA=BG.∴CA=CG.…
∵AE⊥l,CD⊥l,
∴CD∥AE.
∴△GCD∽△GAE.
∴
 .
.
∴AE=2CD.
(3)解:当点F在线段AB上时,如图2,
过点C作CG∥l交AB于点H,交AE于点G.
∴∠2=∠HCB.
∵∠1=∠2,
∴∠1=∠HCB.
∴CH=BH.
∵∠ACB=90°,
∴∠3+∠1=∠HCB+∠4=90°.
∴∠3=∠4.
∴CH=AH=BH.
∵CG∥l,
∴△FCH∽△FEB.
∴
 .
.
设CH=5x,BE=6x,则AB=10x.
∴在△AEB中,∠AEB=90°,AE=8x.
由(2)得,AE=2CD.
∵CD=4,
∴AE=8.
∴x=1.
∴AB=10,BE=6,CH=5.
∵CG∥l,
∴△AGH∽△AEB.
∴
 .
.
∴HG=3.…
∴CG=CH+HG=8.
∵CG∥l,CD∥AE,
∴四边形CDEG为平行四边形.
∴DE=CG=8.
∴BD=DE﹣BE=2.…
当点F在线段BA的延长线上时,如图3,
同理可得CH=5,GH=3,BE=6.
∴DE=CG=CH﹣HG=2.
∴BD=DE+BE=8.
∴BD=2或8.


【点评】本题考查了相似形综合知识,题目中还涉及到了相似三角形的判定与性质及解直角三角形的知识,难度较大,此类题目应重点掌握.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案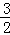 x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( ) |+2cos30°+(9﹣
|+2cos30°+(9﹣ )0+
)0+ .
.


 B.
B.
 C.
C.
 D.
D.


 = .
= . 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )