题目内容
14.例:解方程x4-7x2+12=0解:设x2=y,则x4=y2,∴原方程可化为:y2-7y+12=0,解得y1=3,y2=4,
当y=3时,x2=3,x=±$\sqrt{3}$,当y=4时,x2=4,x=±2.
∴原方程有四个根是:x1=$\sqrt{3}$,x2=-$\sqrt{3}$,x3=2,x4=-2.
以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:(x2+x-2)(x2+x-3)=2;
(2)已知a、b、c是Rt△ABC的三边(c为斜边),S△ABC=6,且a、b满足(a2+b2)2-21(a2+b2)-100=0,试求Rt△ABC的周长.
分析 (1)设x2+x-3=y,则x2+x-2=y+1,由此可得出y2+y-2=0,解之即可得出y的值,再将y值代入x2+x-3=y中求出x值即可;
(2)设a2+b2=x,则x2-21x-100=0,解之可求出x的值,再根据a、b、c是Rt△ABC的三边(c为斜边),结合勾股定理以及S△ABC=6,即可得出a+b与c的值,将其相加即可得出结论.
解答 解:(1)设x2+x-3=y,则x2+x-2=y+1,
∴原方程可化为:(y+1)•y=2,即y2+y-2=0,
解得y1=-2,y2=1.
当y=-2时,x2+x-3=-2,即x2+x-1=0,
解得:x1=$\frac{-1-\sqrt{5}}{2}$,x2=$\frac{\sqrt{5}-1}{2}$;
当y=1时,x2+x-3=1,即x2+x-4=0,
解得:x3=$\frac{-1-\sqrt{17}}{2}$,x4=$\frac{-1+\sqrt{17}}{2}$.
∴原方程有四个根是:x1=$\frac{-1-\sqrt{5}}{2}$,x2=$\frac{\sqrt{5}-1}{2}$,x3=$\frac{-1-\sqrt{17}}{2}$,x4=$\frac{-1+\sqrt{17}}{2}$.
(2)设a2+b2=x,
∴原方程可化为:x2-21x-100=0,解得:x1=25,x2=-4.
∵a、b、c是Rt△ABC的三边(c为斜边),S△ABC=6,
∴a、b、c均为正数,
∴c2=a2+b2=25,ab=12,
∴a+b=$\sqrt{{a}^{2}+{b}^{2}+2ab}$=7,c=5,
∴Rt△ABC的周长为a+b+c=7+5=12.
点评 本题换元法解一元二次方程以及勾股定理,熟练掌握换元法解一元二次方程的方法及步骤是解题的关键.



 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x的值.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x的值. 如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(1,1),
如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(1,1),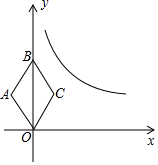 如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.