题目内容
6.如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2$\sqrt{5}$,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.

分析 (1)如图①中,结论:AF=$\sqrt{2}$AE,只要证明△AEF是等腰直角三角形即可;
(2)①如图②中,结论:AF=$\sqrt{2}$AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可;
②分两种情形a、如图③中,当AD=AC时,四边形ABFD是菱形.b、如图④中当AD=AC时,四边形ABFD是菱形.分别求解即可;
解答 解:(1)如图①中,结论:AF=$\sqrt{2}$AE.
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF=$\sqrt{2}$AE.
故答案为AF=$\sqrt{2}$AE.
(2)①如图②中,结论:AF=$\sqrt{2}$AE.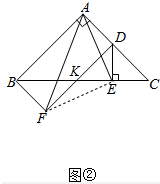
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴∠EKF=180°-∠DKE=135°,EK=ED,
∵∠ADE=180°-∠EDC=180°-45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
$\left\{\begin{array}{l}{EK=ED}\\{∠EKF=∠ADE}\\{KF=AD}\end{array}\right.$,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF=$\sqrt{2}$AE.
②如图③中,当AD=AC时,四边形ABFD是菱形,设AE交CD于H,易知EH=DH=CH=$\sqrt{2}$,AH=$\sqrt{(2\sqrt{5})^{2}-(\sqrt{2})^{2}}$=3$\sqrt{2}$,AE=AH+EH=4$\sqrt{2}$,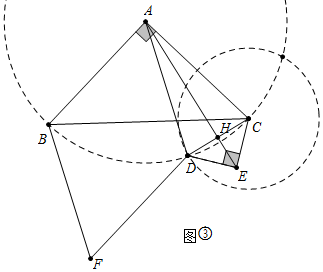
如图④中当AD=AC时,四边形ABFD是菱形,易知AE=AH-EH=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
综上所述,满足条件的AE的长为4$\sqrt{2}$或2$\sqrt{2}$.
点评 本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,寻找全等的条件是解题的难点,属于中考常考题型.

| 进价(元/台) | 售价(元/台) | |
| 电饭煲 | 200 | 250 |
| 电压锅 | 160 | 200 |
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的$\frac{5}{6}$,问橱具店有哪几种进货方案?全部售完时,哪种进货方案盈利最多?
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
(2)全部售完100只节能灯后,该商场获利多少元?
 将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.
将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.