题目内容
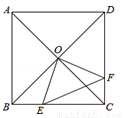
(本题满分8分)如图,在 中,
中, ,
, 平分
平分 交
交 于点
于点 ,点
,点 在
在 边上且
边上且 .
. 
(1)判断直线 与
与 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;
(2)若 ,
, ,求
,求 的长.
的长.
(1)相切,证明垂直即可,过程见解析;(2)
解析试题分析:(1)可先观察图,猜想位置关系为相切,而要证明相切,需证得垂直,故取 的中点
的中点 ,联结
,联结 后,结合两半径构成的等腰三角形性质和角平分线定义,易证得确为垂直关系;(2)由(1)的结论,根据勾股定理构造方程,可求出半径长,再求出直径
后,结合两半径构成的等腰三角形性质和角平分线定义,易证得确为垂直关系;(2)由(1)的结论,根据勾股定理构造方程,可求出半径长,再求出直径 长.
长.
试题解析:(1)直线 与
与 外接圆相切,理由如下:
外接圆相切,理由如下:
取 的中点记为
的中点记为 ,联结
,联结 ,则
,则

 平分
平分





 与
与 外接圆相切.
外接圆相切.
(2)由(1)得  为直角三角形,故
为直角三角形,故
设 ,则
,则  解得
解得

考点:1.圆切线的定义及性质;2.平行线的判定及性质;3.勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O的半径为7cm,OA=5cm,那么点A与⊙O的位置关系是( )
| A.在⊙O内 | B.在⊙O上 | C.在⊙O外 | D.不能确定 |
 2的一元一次方程(只写一个即可):____________________.
2的一元一次方程(只写一个即可):____________________.
 ,求DG的长.
,求DG的长. .
. 
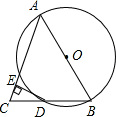
 ,∠DPA=45°.
,∠DPA=45°.