题目内容
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=DB,连结AC,过点D作DE⊥AC于E.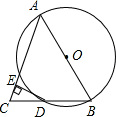
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(1)证明见解析;(2)证明见解析.
解析试题分析:(1)连接AD,根据中垂线定理不难求得AB=AC;
(2)要证DE为⊙O的切线,只要证明∠ODE=90°即可.
试题解析:(1)连接AD;
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,
∴AD是BC的中垂线.
∴AB=AC.
(2)连接OD;
∵OA=OB,CD=BD,
∴OD∥AC.
∴∠0DE=∠CED.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
考点:1.切线的判定;2.等腰三角形的性质;3.圆周角定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目


 中,
中, ,
,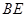 平分
平分 交
交 于点
于点 ,点
,点 在
在 边上且
边上且 .
. 
 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;  ,
, ,求
,求 的长.
的长.
