题目内容
12.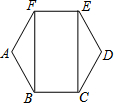 如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为( )
如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为( )| A. | 20$\sqrt{3}$ | B. | 40 | C. | 20$\sqrt{5}$ | D. | 45 |
分析 连接AD交BF、CE与M、N,根据正多边形的性质求出∠FAB=120°,根据三角形的面积公式计算即可.
解答 解: 连接AD交BF、CE与M、N,
连接AD交BF、CE与M、N,
∵正六边形ABCDEF,
∴∠FAB=120°,
∴∠FAM=60°,
∴AM=$\frac{1}{2}$AF,
∴AM=$\frac{1}{2}$EF,
∴△FAB的面积=$\frac{1}{4}$×四边形BCEF的面积=7.5,
同理△EDC的面积=7.5,
∴正六边形ABCDEF的面积=30+7.5+7.5=45,
故选:D.
点评 本题考查的是正多边形与圆,掌握正多边形的性质、正多边形的中心角的求法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
 如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )| A. | 25° | B. | 65° | C. | 105° | D. | 115° |
1.下列说法正确的是( )
| A. | 4的平方根是-2 | B. | 8的立方根是±2 | ||
| C. | 任何实数都有平方根 | D. | 任何实数都有立方根 |
2.在直角坐标系中与(2,-3)在同一个正比例函数图象上的是( )
| A. | (2,3) | B. | (-2,-3) | C. | (4,-6) | D. | (-4,-6) |
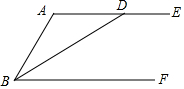 已知BD平分∠ABF,且交AE于点D.
已知BD平分∠ABF,且交AE于点D.