题目内容
如图，将以A为直角顶点的等腰直角三角形ABC沿直线BC平移到△A′B′C′，使点B′与C重合，连接AC′，若AB=a，求AC′的长．考点：平移的性质,勾股定理,等腰直角三角形
专题：
分析：作AE⊥BC交BC于E，首先根据△ABC是等腰直角三角形，AB=a，得到AE的长，然后利用勾股定理求得结论即可．
解答：
解：作AE⊥BC交BC于E，
∵△ABC是等腰直角三角形，AB=a，
∴AE=BE=
a，
∴EC′=
a，
∴由勾股定理得：AC′=
=
a，
∴AC′的长为
a．
解：作AE⊥BC交BC于E，∵△ABC是等腰直角三角形，AB=a，
∴AE=BE=
| ||
| 2 |
∴EC′=
3
| ||
| 2 |
∴由勾股定理得：AC′=
(
|
| 5 |
∴AC′的长为
| 5 |
点评：本题考查了平移的性质、勾股定理及等腰直角三角形的知识，属于基础题，难度较小．
练习册系列答案
相关题目
如图，已知函数y=kx+b和y=kx的图象交于点P，则根据图象可得关于x，y的二元一次方程组
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
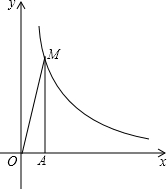反比例函数y=
如图，在坡角为30°的山坡上有一铁塔AB，其正前方矗立着一大型广告牌，当阳光与水平线成45°角时，测得铁塔AB落在斜坡上的影子BD的长为6米，落在广告牌上的影子CD的长为4米，求铁塔AB的高（AB，CD均与水平面垂直，结果保留根号）．
在平面直角坐标系中xOy中，点A与原点O重合，点B（4，0），点E、（0，2），过点E作平行于x轴的直线l，点C、D在直线上运动（点C在点D的左侧），CD=4，连接BC，过点A作关于直线BC的对称点A′，连接AC、A′C．