题目内容
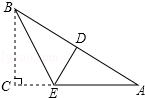如图，在三角形纸片ABC中，∠C=90°，AC=6，折叠该纸片，使点C落在AB边上的D点处，折痕BE与AC交于点E，若AD=BD，则折痕BE的长为（ ）| A、1 | B、2 | C、3 | D、4 |
考点：翻折变换（折叠问题）
专题：
分析：根据题意结合图形首先求出∠A度数，进而求出∠CBE的度数，通过解直角△BCE即可解决问题．
解答：解：由题意得：△BCE≌△BDE，
∴∠BDE=∠C=90°，BD=BC；
又∵AD=BD，
∴DE⊥AB，且平分AB，
∴BE=AE（设为x）；
∵AB=BD=BC，
∴AB=2BC，而∠C=90°，
∴∠A=30°，∠ABC=60°，
∴∠CBE=
∠ABC=30°，
∴BE=2CE；
∵BE=x，CE=6-x，
∴x=2（6-x），
解得：x=4，
故该题答案为D．
解：由题意得：△BCE≌△BDE，∴∠BDE=∠C=90°，BD=BC；
又∵AD=BD，
∴DE⊥AB，且平分AB，
∴BE=AE（设为x）；
∵AB=BD=BC，
∴AB=2BC，而∠C=90°，
∴∠A=30°，∠ABC=60°，
∴∠CBE=
| 1 |
| 2 |
∴BE=2CE；
∵BE=x，CE=6-x，
∴x=2（6-x），
解得：x=4，
故该题答案为D．
点评：该命题以三角形为载体，通过翻折变换重点考查了全等三角形的性质及其应用、直角三角形的边角关系等几何知识点；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
在-1
，12，-20，0，-（-5）中，负数的个数有（ ）
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，有一圆柱，其高为12cm，它的底面半径为3cm，在圆柱下底面A处有一只蚂蚁，它想得到上面B处的食物，则蚂蚁经过的最短距离为（ ）cm．（π取3）