题目内容
因式分解.
(1)x4-3x2+1;
(2)x4-7x2y2+81y4.
(1)x4-3x2+1;
(2)x4-7x2y2+81y4.
考点:因式分解
专题:
分析:(1)利用拆项法将-3x2分成两部分,进而利用完全平方公式以及平方差公式分解因式得出即可;
(2)利用补项法进而利用完全平方公式以及平方差公式分解因式得出即可.
(2)利用补项法进而利用完全平方公式以及平方差公式分解因式得出即可.
解答:解:(1)x4-3x2+1
=(x2)2-2x2+1-x2
=(x2-1)2-x2
=(x2+x-1)(x2-x-1);
(2)原式=(x2)2+18x2y2+(9y2)2-25x2y2
=(x2+9y2)2-(5xy)2
=(x2+9y2+5xy)(x2+9y2-5xy).
=(x2)2-2x2+1-x2
=(x2-1)2-x2
=(x2+x-1)(x2-x-1);
(2)原式=(x2)2+18x2y2+(9y2)2-25x2y2
=(x2+9y2)2-(5xy)2
=(x2+9y2+5xy)(x2+9y2-5xy).
点评:本题考查了提公因式法、公式法分解因式,正确利用拆项和补项法分解因式是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知a、b满足方程组
,则a-b的值为( )
|
| A、-1 | B、m-1 | C、0 | D、1 |
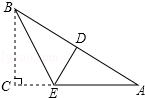 如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为( )
如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为( ) 如图所示,在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,∠DAB的平分线交DE于点M,交DF于点N,交DC于点P.求证:DM=DN.
如图所示,在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,∠DAB的平分线交DE于点M,交DF于点N,交DC于点P.求证:DM=DN. 如图,⊙O的直径AB=10cm,∠CBD=45°,求弦CD的长.
如图,⊙O的直径AB=10cm,∠CBD=45°,求弦CD的长.