题目内容
19．
如图，∠1=∠2，∠A=∠C．（1）求证：AD∥BC；
（2）若∠A=50°，则∠CBE的度数是50°．
分析 （1）根据三角形的内角和定理得到∠ADB=∠CBD，然后根据平行线的判定即可得到结论；
（2）根据平行线的性质即可得到结果．
解答 解：（1）∵∠1=∠2，∠A=∠C，
∴180°-∠1-∠C=180°-∠2-∠A，
∴∠ADB=∠CBD，
∴AD∥CB；
（2）∵AD∥CB，
∴∠CBE=∠A=50°．
故答案为：50°．
点评 本题主要考查了平行线的性质和判定定理，熟记定理是解答此题的关键．
练习册系列答案
相关题目
如图，平面直角坐标系中，三角形ABC的顶点都在网格点上，平移三角形ABC，使点B与坐标原点O重合．请写出图中点A，B，C的坐标并画出平移后的三角形A1OC1．
7．
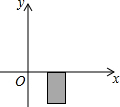在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是（ ）
在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是（ ）| A． | （-3，300） | B． | （7，-500） | C． | （9，600） | D． | （-2，-800） |
4．
如图，直线l1，l2，被l3所截得的同旁内角为α，β，要使l1∥l2，只要使（ ）
如图，直线l1，l2，被l3所截得的同旁内角为α，β，要使l1∥l2，只要使（ ）| A． | α+β=90° | B． | α=β | C． | $\frac{1}{5}α+\frac{1}{5}β$=36° | D． | α+β=360° |
如图，AB∥CD，直线EF分别交AB、CD于点E、F，FH平分∠EFD，如果∠1=108°，求∠2的度数．
9．
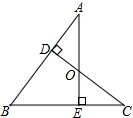如图，AE与CD相交于点O，∠ADO=∠CEO=90°，下列条件中，不能证明△AOD≌△COE的是（ ）
如图，AE与CD相交于点O，∠ADO=∠CEO=90°，下列条件中，不能证明△AOD≌△COE的是（ ）| A． | AO=CO | B． | DO=EO | C． | AD=CE | D． | ∠A=∠C |