题目内容
11. 如图,AB∥CD,直线EF分别交AB、CD于点E、F,FH平分∠EFD,如果∠1=108°,求∠2的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,FH平分∠EFD,如果∠1=108°,求∠2的度数.
分析 根据角平分线定义得出∠EFH=∠HFD,根据平行线性质得出∠1+∠EFD=180°,∠2=∠HFD,求出∠EFD和∠HFD即可.
解答 解:∵FH平分∠EFD,
∴∠EFH=∠HFD,
∵AB∥CD,
∴∠1+∠EFD=180°,
∵∠1=108°,
∴∠EFD=72°,
∴∠EFH=∠HFD=$\frac{1}{2}$∠EFD=36°,
∵AB∥CD,
∴∠2=∠HFD=36°.
点评 本题考查了平行线的性质,角平分线定义的应用,能根据平行线的性质进行推理是解此题的关键,注意:①两直线平行,内错角相等,②两直线平行,同旁内角互补.

练习册系列答案
相关题目
16.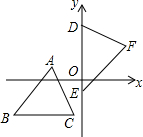 如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )
如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )
 如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )
如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.一个等腰三角形的两边长分别是4和9,则它的周长为( )
| A. | 17 | B. | 20 | C. | 22 | D. | 17或22 |
 如图,∠1=∠2,∠A=∠C.
如图,∠1=∠2,∠A=∠C.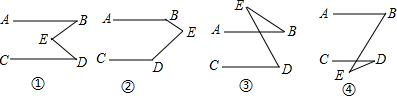
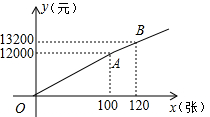 为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.
为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.