题目内容
若实数x、y满足x2+y2-4x-2y+5=0,则
+
的值是( )
| x |
| y |
| A、3 | ||
| B、1 | ||
C、
| ||
D、
|
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:首先把x2+y2-4x-2y+5=0变为(x-2)2+(y-1)2=0,利用非负数的性质得出x、y的数值,进一步代入求得答案按即可.
解答:解:∵x2+y2-4x-2y+5=0,
∴(x-2)2+(y-1)2=0,
∴x-2=0,y-1=0,
∴x=2,y=1,
∴
+
=
+1.
故选:C.
∴(x-2)2+(y-1)2=0,
∴x-2=0,y-1=0,
∴x=2,y=1,
∴
| x |
| y |
| 2 |
故选:C.
点评:此题考查因式分解的运用,非负数的性质,注意利用完全平方公式分组分解是解决问题的关键.

练习册系列答案
相关题目
式子:-x+1,x+3,
,S=
ab中,整式的个数是( )
| x |
| x+y |
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
 已知等腰直角△ABC与等腰直角△ADE,F是EC中点,问:DF与BF的关系?并证明你的猜想.
已知等腰直角△ABC与等腰直角△ADE,F是EC中点,问:DF与BF的关系?并证明你的猜想. 如图,∠1与∠3是同位角吗?∠2与∠4是同位角吗?
如图,∠1与∠3是同位角吗?∠2与∠4是同位角吗?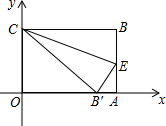 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=