题目内容
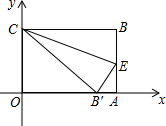 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=| 3 |
| 4 |
(1)求B′点和B点的坐标;
(2)若双曲线过点E,求双曲线的解析式,以及双曲线与直线CB的交点F的坐标.
考点:反比例函数综合题
专题:
分析:(1)利用三角函数和翻折不变性求出AO、AB的长即可求出B′点和B点的坐标;
(2)在Rt△EAB′中,利用勾股定理求出AE的长即可求出E点坐标,然后利用待定系数法求出反比例函数解析式,即可求出直线CB的交点F的坐标.
(2)在Rt△EAB′中,利用勾股定理求出AE的长即可求出E点坐标,然后利用待定系数法求出反比例函数解析式,即可求出直线CB的交点F的坐标.
解答:解:(1)在Rt△COB′中,CO=9,tan∠OB′C=
,
则
=
,
即
=
,
解得OB′=12,B′坐标为(12,0),
CB′=
=15,
由翻折不变性可知CB=CB′=15,即AO=15,
B坐标为(12,9).
(2)由(1)可知AB′=15-12=3,
设AE=a,则B′E=BE=9-a,
在Rt△EAB′中,
32+a2=(9-a)2,
解得a=4,
E点坐标为(15,4),
设过E的反比例函数解析式为y=
,
把(15,4)代入上式得,k=60,
解析式为y=
,
当y=9时,
=9,
解得x=
,
即F点的坐标为(
,9).
| 3 |
| 4 |
则
| CO |
| OB′ |
| 3 |
| 4 |
即
| 9 |
| OB′ |
| 3 |
| 4 |
解得OB′=12,B′坐标为(12,0),
CB′=
| 92+122 |
由翻折不变性可知CB=CB′=15,即AO=15,
B坐标为(12,9).
(2)由(1)可知AB′=15-12=3,
设AE=a,则B′E=BE=9-a,
在Rt△EAB′中,
32+a2=(9-a)2,
解得a=4,
E点坐标为(15,4),
设过E的反比例函数解析式为y=
| k |
| x |
把(15,4)代入上式得,k=60,
解析式为y=
| 60 |
| x |
当y=9时,
| 60 |
| x |
解得x=
| 20 |
| 3 |
即F点的坐标为(
| 20 |
| 3 |
点评:本题考查了反比例函数综合知识,将反比例函数与翻折变换、勾股定理相结合,有一定的难度.

练习册系列答案
相关题目
若实数x、y满足x2+y2-4x-2y+5=0,则
+
的值是( )
| x |
| y |
| A、3 | ||
| B、1 | ||
C、
| ||
D、
|
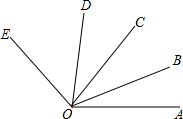 如图,∠AOD=α,∠AOB=∠COD=β,∠COE=γ.请用α、β、γ表示∠BOE.
如图,∠AOD=α,∠AOB=∠COD=β,∠COE=γ.请用α、β、γ表示∠BOE.