题目内容
二次函数的顶点是(2,-1),该抛物线可设为 .
考点:二次函数的三种形式
专题:
分析:已知抛物线的顶点坐标,则可以设该解析式为顶点式.
解答:解:∵二次函数的顶点是(2,-1),
∴该抛物线可设为 y=a(x-2)-1(a≠0).
故答案是:y=a(x-2)-1(a≠0).
∴该抛物线可设为 y=a(x-2)-1(a≠0).
故答案是:y=a(x-2)-1(a≠0).
点评:本题考查了抛物线的三种形式.顶点式:y=a(x-h)2+k(a是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若实数x、y满足x2+y2-4x-2y+5=0,则
+
的值是( )
| x |
| y |
| A、3 | ||
| B、1 | ||
C、
| ||
D、
|
已知a-b=1,b-c=2,那么代数式(a-c)2-2(c-a)+1的值为( )
| A、12 | B、14 | C、16 | D、18 |
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于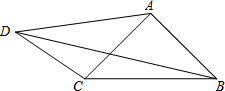 如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为
如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为