题目内容
 已知等腰直角△ABC与等腰直角△ADE,F是EC中点,问:DF与BF的关系?并证明你的猜想.
已知等腰直角△ABC与等腰直角△ADE,F是EC中点,问:DF与BF的关系?并证明你的猜想.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:易证∠DEF=∠NCF,即可证明△FDE≌△FMC,可得DF=MF,DE=MC,即可求得AD=MC,易证∠DAB=∠MCB,即可证明△BCM≌△BAD,可得BM=BD,∠ABD=∠CBM,根据∠ABD+∠DBC=90°即可求得∠DBM=90°,可证明△DBM是等腰直角三角形,根据等腰直角三角形底边三线合一性质即可解题.
解答:证明:过点C作CM∥ED,与DF的延长线交于点M,连接BD,BM,

∵CM∥ED,
∴∠DEF=∠NCF,
在△FDE和△FMC中,
,
∴△FDE≌△FMC﹙ASA﹚,
∴DF=MF,DE=MC,
∴F是DM中点,
∵AD=DE,
∴AD=ED=MC,
∵DE∥CM,BC⊥AB,
∴∠DAB=∠MCB,
∵在△BCM和△BAD中,
,
∴△BCM≌△BAD(SAS),
∴BM=BD,∠ABD=∠CBM,
∵∠ABD+∠DBC=90°,
∴∠DBC+∠CBM=90°,即∠DBM=90°,
∴△DBM是等腰直角三角形,
∵F是DM的中点,
∴△BFD是等腰直角三角形;
∴DF=BF,DF⊥BF.

∵CM∥ED,
∴∠DEF=∠NCF,
在△FDE和△FMC中,
|
∴△FDE≌△FMC﹙ASA﹚,
∴DF=MF,DE=MC,
∴F是DM中点,
∵AD=DE,
∴AD=ED=MC,
∵DE∥CM,BC⊥AB,
∴∠DAB=∠MCB,
∵在△BCM和△BAD中,
|
∴△BCM≌△BAD(SAS),
∴BM=BD,∠ABD=∠CBM,
∵∠ABD+∠DBC=90°,
∴∠DBC+∠CBM=90°,即∠DBM=90°,
∴△DBM是等腰直角三角形,
∵F是DM的中点,
∴△BFD是等腰直角三角形;
∴DF=BF,DF⊥BF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△FDE≌△FMC和△BCM≌△BAD是解题的关键.

练习册系列答案
相关题目
若实数x、y满足x2+y2-4x-2y+5=0,则
+
的值是( )
| x |
| y |
| A、3 | ||
| B、1 | ||
C、
| ||
D、
|
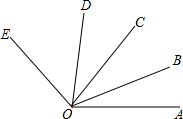 如图,∠AOD=α,∠AOB=∠COD=β,∠COE=γ.请用α、β、γ表示∠BOE.
如图,∠AOD=α,∠AOB=∠COD=β,∠COE=γ.请用α、β、γ表示∠BOE.