题目内容

6．已知∠A的两边与∠B的两边分别平行，且∠A比∠B的3倍少40°，那么∠A=20°或125°．

分析 设∠B的度数为x，则∠A的度数为3x-40°，根据两边分别平行的两个角相等或互补得到x=3x-40°或x+3x-40°=180°，再分别解方程，然后计算3x-40°的值即可．

解答 解：设∠B的度数为x，则∠A的度数为3x-40°，
当∠A=∠B时，即x=3x-40°，解得x=20°，所以3x-40°=20°；
当∠A+∠B=180°时，即x+3x-40°=180°，解得x=55°，所以3x-40°=125°；
所以∠A的度数为20°或125°．
故答案为：20°或125．

点评 本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．也考查了两边分别平行的两个角的关系．关键是分类讨论．

练习册系列答案
相关题目
16．若|a-3|=3-a，则a=2（答案不唯一）．（请写一个符合条件a的值）
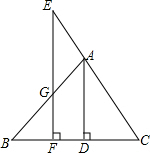17．如图，已知AD⊥BC于点D，EF⊥BC于点F，交AB于点G，交CA的延长线于点E，∠E=∠AGE，求证：∠BAD=∠CAD．
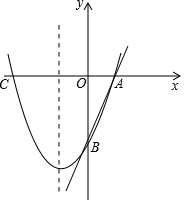14．如图，已知直线y=3x-3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过
A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．
（1）求抛物线的解析式：
（2）求△ABC的面积；
（3）在抛物线的对称轴上，是否存在点M，使△ABM周长最短？若不存在，请说明理由；若存在，求出点M的坐标．
1．给出如下规定：两个图形G1和G2，点P为G1上任一点，点Q为G2上任一点，如果线段PQ的长度存在最小值，就称该最小值为两个图形G1和G2之间的距离．在平面直角坐标系xOy中，O为坐标原点．
（1）点A的坐标为A（1，0），则点B（2，3）和射线OA之间的距离为3，点C（-2，3）和射线OA之间的距离为$\sqrt{13}$；
（2）如果直线y=x+1和双曲线y=$\frac{k}{x}$之间的距离为$\frac{3\sqrt{2}}{2}$，那么k=-4；（可在图1中进行研究）
（3）点E的坐标为（1，$\sqrt{3}$），将射线OE绕原点O顺时针旋转120°，得到射线OF，在坐标平面内所有和射线OE，OF之间的距离相等的点所组成的图形记为图形M．
①请在图2中画出图形M，并描述图形M的组成部分；（若涉及平面中某个区域时可以用阴影表示）．
②将射线OE，OF组成的图形记为图形W，直线y=-2x-4与图形M的公共部分记为图形N，请求出图形W和图形N之间的距离．
11．抛物线C：y=$\frac{1}{4}$x2+bx+c的顶点（1，-2）
（1）求抛物线C的解析式；
（2）直线l：y=kx+b与抛物线C交于A、B两点
①当b=-4时，若线段AB被x轴平分，求k的值；
②当k=1时，若线段AB=4$\sqrt{10}$，求b的值；
（3）抛物线C的顶点平移到原点，得新抛物线C1，抛物线C1上一点M（-4，t），过点M作抛物线的两条弦MD和MC，且MD⊥MC，判断直线DC是否过定点？并说明理由．
18．（1）如图1，P为正方形ABCD的AD边上一点，PE⊥AD交BD于E点，将△PCD绕C点逆时针方向旋转90°到△FCB的位置，连接PF交BD于Q点．
①求证：BQ=EQ；②探究线段PQ与线段CQ的关系，并证明你的结论；
（2）再将△PED绕D点顺时针方向旋转45°，再将△PDC绕C点逆时针方向旋转90°至△FBC处（如图2），（1）中你探究的结论：线段PQ与线段CQ的关系是否依然成立？若成立，写出结论并予以证明；若不成立，请说明理由；
（3）若将△PED绕D点顺时针方向旋转α（0°＜α＜90°），其它条件不变，试画图并判断线段PQ与线段CQ的关系（直接写出结论，不证明）．
9．某工厂生产了一大批产品，从中随机抽取了16件来检查，发现有2件次品，则这批产品的次品率约为$\frac{1}{8}$，合格率约为$\frac{7}{8}$．（用分数表示）
10．下列各组式子中，是同类项的是（　　）
A．3x2y与-3xy2B．5xy与5yzC．2x与2x2D．3xy与-2yx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网