题目内容
18.在△ABC中,∠C=90°,AC=3,BC=4,求△ABC的内切圆⊙O的半径.分析 由切线长定理得出AE=AD,CE=CF,BD=BF;证出四边形OECF是正方形,则列方程即可求得⊙O的半径r.
解答 解:连接圆心O和各个切点,如图所示.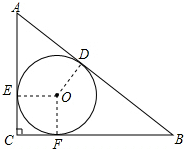
∵Rt△ABC中,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵⊙O为△ABC的内切圆,
∴AE=AD,CE=CF,BD=BF,OE⊥AC,OF⊥BC,
∴∠OFC=∠OEC=∠C=90°,
∴四边形OECF是矩形;
∵OE=OF,
∴四边形OECF是正方形;
∵⊙O的半径为r,
∴CE=CF=r,AE=AD=3-r,BD=BF=4-r,
∴3-r+4-r=5,
解得:r=1,
∴△ABC的内切圆的半径r=1.
点评 此题考查了三角形内切圆的性质、切线长定理、勾股定理、正方形的判定;熟练掌握切线长定理,证明四边形是正方形是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.一元二次方程x2+x-6=0的根的情况是( )
| A. | 有两个相等的实根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实根 | D. | 无法确定 |

 如图,点D在AC的垂直平分线上,AB∥CD,若∠D=130°,则∠BAC的度数是25°.
如图,点D在AC的垂直平分线上,AB∥CD,若∠D=130°,则∠BAC的度数是25°.