题目内容
8. 如图,在△ABC中,以AC为边在△ABC外作正△ACD,连接BD.
如图,在△ABC中,以AC为边在△ABC外作正△ACD,连接BD.(1)以点A为中心,把△ADB顺时针旋转60°,画出旋转后的图形(保留作图痕迹);
(2)若∠ABC=30°,BC=4,BD=6,求AB的长.
分析 (1)由于△ACD为等边三角形,则AC=AD,∠DAC=60°,则作∠BAE=60°,再截取AE=AB,于是△ACE可由△ADB绕点A顺时针旋转60°得到;
(2)连结BE,如图,根据旋转的性质得BD=CE=6,AE=AB,∠BAE=60°,可判断△ABE为等边三角形,所以∠ABE=60°,BE=AB,加上∠ABC=30°,所以∠EBC=90°,然后利用勾股定理计算出BE.从而得到AB的长.
解答 解:(1)如图,△ACE为所作;
(2)连结BE,如图,
∵△ABD绕点A顺时针旋转60°得到△AEC,
∴BD=CE=6,AE=AB,∠BAE=60°,
∴△ABE为等边三角形,
∴∠ABE=60°,BE=AB,
而∠ABC=30°,
∴∠EBC=90°,
在Rt△ABE中,BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴AB=2$\sqrt{5}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
20.在-(-8),(-1)2007,-32,0,-|-1|,-$\frac{2}{5}$中,负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a-b)2=a2-b2 | C. | -(3ab3)2=-6a2b6 | D. | -2x-2=-$\frac{2}{x^2}$ |
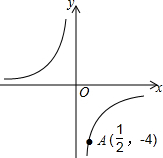 反比例函数y=$\frac{k}{x}$的图象如图所示.
反比例函数y=$\frac{k}{x}$的图象如图所示. 如图,一只小蚂蚁要在正方体的表面从顶点A爬到距A最远的另一个顶点B.哪条路径最短?这样的最短路径有多少条?请说明理由.
如图,一只小蚂蚁要在正方体的表面从顶点A爬到距A最远的另一个顶点B.哪条路径最短?这样的最短路径有多少条?请说明理由. 如图,直线AB,CD相交于点O,∠BOE:∠DOE=1:2,OF⊥OE,∠AOC=60°,求∠DOF的度数.
如图,直线AB,CD相交于点O,∠BOE:∠DOE=1:2,OF⊥OE,∠AOC=60°,求∠DOF的度数.