题目内容
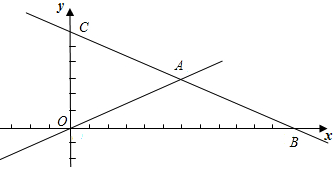
6.如图,在平面直角坐标系中,直线L1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B,C,且与直线L2:y=$\frac{1}{2}$x交于点A.(1)分别求出点A、B、C的坐标;(2)若D是线段OA上的点且△COD的面积为12,求直线CD的表达式;
(3)在(2)的条件下,在射线CD上是否存在点P使△OCP为等腰三角形?若存在,直接写出点P的坐标.若不存在,请说明理由.
分析 (1)联立两直线解析式可求得A点坐标,利用直线L1的解析式可求得B、C的坐标;
(2)可设D(x,$\frac{1}{2}$x),由题意可求得x的值,则可求得D点坐标,利用待定系数法可求得直线CD的表达式;
(3)可设出P点坐标,利用勾股定理可表示出PC、PO和OC的长,分PC=PO、PC=OC和PO=OC三种情况,分别得到关于P点坐标的方程,可求得P点坐标.
解答 解:
(1)联立两直线解析式可得$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=\frac{1}{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$,
∴A(6,3),
在y=-$\frac{1}{2}$x+6中,令y=0可求得x=12,令x=0可得y=6,
∴B(12,0),C(0,6);
(2)∵点D在线段OA上,
∴可设D(x,$\frac{1}{2}$x)(0≤x≤6),
∵△COD的面积为12,
∴$\frac{1}{2}$×6x=12,解得x=4,
∴D(4,2),
∵C(0,6),
∴可设直线CD的表达式为y=kx+6,
把D(4,2)代入可得4=2k+6,解得k=-1,
∴直线CD的表达式为y=-x+6;
(3)∵点P在射线CD上,
∴可设P(t,-t+6)(t≥0),
∵C(0,6),O(0,0),
∴PC=$\sqrt{{t}^{2}+(-t+6-6)^{2}}$=$\sqrt{2}$t,OP=$\sqrt{{t}^{2}+(-t+6)^{2}}$=$\sqrt{2{t}^{2}-12t+36}$,且OC=6,
∵△OCP为等腰三角形,
∴有PC=PO、PC=OC和PO=OC三种情况,
①当PC=PO时,即$\sqrt{2}$t=$\sqrt{2{t}^{2}-12t+36}$,解得t=3,此时P点坐标为(3,3);
②当PC=OC时,即$\sqrt{2}$t=6,解得t=3$\sqrt{2}$,此时P点坐标为(3$\sqrt{2}$,6-3$\sqrt{2}$);
③当PO=OC时,即$\sqrt{2{t}^{2}-12t+36}$=6,解得t=0或t=6,当t=0时,P与O重合,不合题意,舍去,故t=6,此时P点坐标为(6,0);
综上可知存在满足条件的点P,其坐标为(3,3)或(3$\sqrt{2}$,6-3$\sqrt{2}$)或(6,0).
点评 本题为一次函数的综合应用,涉及待定系数法、函数图象的交点、三角形的面积、勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识.在(1)中注意函数图象的交点坐标的求法,在(2)中求得D点坐标是解题的关键,在(3)中用P点坐标分别表示出PO和PC是解题的关键,注意分类讨论.本题考查知识点较多,综合性较强,难度适中.

| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | … | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | 1 | $\frac{3}{2}$ | 3 | 6 | … | -6 | -3 | -$\frac{3}{2}$ | -1 | … |
| A. | 图象在第二、四象限内 | B. | 图象必经过点(6,-$\frac{1}{2}$) | ||
| C. | 图象与坐标轴没有交点 | D. | 当x<-4时,y的取值范围是<$\frac{3}{4}$ |
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{5}$或3 | D. | $\sqrt{5}$或$\sqrt{2}$ |
| A. | x≤2 | B. | x>2 | C. | x≥2 | D. | x<2 |
| A. | 9×10-5米 | B. | 9×10-4米 | C. | 0.9×10-6米 | D. | 90×10-3米 |
| A. | $\left\{\begin{array}{l}{mn=2}\\{m+n=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5m-2n=0}\\{\frac{1}{m}+n=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m+n=0}\\{3m-2a=\frac{1}{6}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=8}\\{\frac{m}{3}-\frac{n}{2}=1}\end{array}\right.$ |
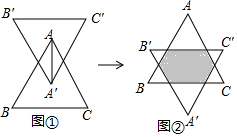 如图①,等边三角形ABC和等边三角形A′B′C′的边长均为2,且BC∥B′C′,将等边三角形ABC沿A′A方向向上平移到图②的位置,则阴影部分的周长为4.
如图①,等边三角形ABC和等边三角形A′B′C′的边长均为2,且BC∥B′C′,将等边三角形ABC沿A′A方向向上平移到图②的位置,则阴影部分的周长为4.