Question

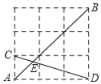
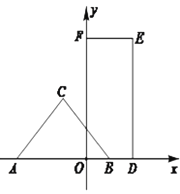
【题目】如图，等腰直角的斜边在x轴上且长为4，点C在x轴上方．矩形中，点D、F分别落在x、y轴上，边长为2，长为4，将等腰直角沿x轴向右平移得等腰直角．

(1)当点与点D重合时，求直线的解析式；

(2)连接，．当线段和线段之和最短时，求矩形和等腰直角重叠部分的面积；

(3)当矩形和等腰直角重叠部分的面积为时，求直线与y轴交点的坐标．(本问直接写出答案即可)

Answer 1

【答案】(1)；(2)S重合=3；(3)．

【解析】

（1）由OD=2，AB=4可得B′与D重合时，点O为AB中点，根据等腰直角三角形的性质可得OC⊥AB，OC′=OD，即可得A′、C′的坐标，利用待定系数法即可得A′C′的解析式；（2）根据等腰三角形的性质可得点在直线上移动，由点F与点O关于y=2得出可得当点，，在同一条直线上时，最小，根据O、E坐标可得直线OE解析式，即可得出C′坐标，进而可得直线的解析式，可得G点坐标，H点坐标，根据S重合=S△ABC-S△OA′G-S△HDB即可得答案；（3）如图，设OA′=x，根据S△A′OM+S△B′DN=S△ABC-S重合列方程即可求出x的值，即可得直线与轴交点的坐标．

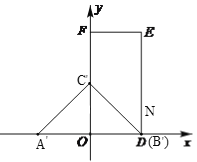
（1）∵点B′与D重合，OD=2，AB=4，

∴OA=OD=2，

∵△A′B′C′是等腰直角三角形，

∴OC′⊥AB，

∴点C′在y轴上，

∴OC′=OD=2，

∴A′（-2，0），C′（0，2）

设A′C′的解析式为y=kx+b，

∴，

解得：，

∴A′C′的解析式为y=x+2.

（2）如图，∵△ABC斜边AB上的高为2，

∴点在直线上移动，

∵点和点关于直线对称．

∴

∴当点，，在同一条直线上时，最小，即此时取得最小值．

设直线OE的解析式为y=kx,

∵E（2,4），

∴4=2k，

解得k=2，

∴直线OE的解析式为y=2x，

∴，

设直线的解析式为，

把(1，2)代入，得b=1

∴直线的解析式为，

当x=0时，y=1，

∴G（0，1），

∴OG=OA′=1，

∴DH=DB′=AB-OA′-OD=1，

∴重叠部分的面积为：.

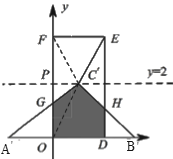
（3）如图，S重合=2.5时，

∴S△A′OM+S△B′DN=S△ABC-S重合=4-2.5=1.5，

设OA′=x，则DB′=2-x(0<x<2)，

∵OA′=OM，DB′=DN，

∴xx+(2-x)2=1.5，

解得：x=，

∴直线与轴交点的坐标为（0，）或（0，）.