题目内容
14.已知△ABC,(1)如图(1),若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+$\frac{1}{2}$∠A;
(2)如图(2),若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;
(3)如图(3),若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-$\frac{1}{2}$∠A.
上述说法正确的个数是( )

| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 用角平分线的性质和三角形内角和定理证明,证明时可运用反例.
解答 解:(1)若P点是∠ABC和∠ACB的角平分线的交点,
则∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB
则∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A)
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,
故成立;
(2)当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
(3)若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC=$\frac{1}{2}$∠FBC=$\frac{1}{2}$(180°-∠ABC)=90°-$\frac{1}{2}$∠ABC,
∠BCP=$\frac{1}{2}$∠BCE=90°-$\frac{1}{2}$∠ACB
∴∠PBC+∠BCP=180°-$\frac{1}{2}$(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°-∠A
∴∠PBC+∠BCP=90°+$\frac{1}{2}$∠A,
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-$\frac{1}{2}$(180°+∠A)=90°-$\frac{1}{2}$∠A,
故成立.
∴说法正确的个数是2个.
故选B.
点评 此题主要考查了三角形的内角和外角之间的关系.
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.

练习册系列答案
相关题目
4.下列各式从左到右的变形正确的是( )
| A. | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B. | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C. | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D. | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,说明它是假命题的反例可以是( )
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=∠2=45° |
6.下列计算正确的是( )
| A. | 4x-9x+6x=-x | B. | a-a=0 | C. | x3-x2=x | D. | xy-2xy=3xy |
4.国庆期间,某公园门票规定如下表:
某校七年级(1)(2)两个班共104人去游园,如果以班为单位购票,共付1240元,其中(1)班人数大于40人小于50人,试问:
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
| 购票人数 | 1-50张 | 51~100张 | 100张以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
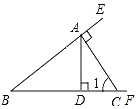 如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:
如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论: 已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.
已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.