题目内容
5.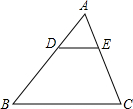 某施工地在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被消去了一个角△ADE,变成了一个梯形BCED,原绿化地一边AB的长由原来的30米缩短成BD长18米,现在的问题是:被消去的部分面积有多大?它的周长是多少?
某施工地在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被消去了一个角△ADE,变成了一个梯形BCED,原绿化地一边AB的长由原来的30米缩短成BD长18米,现在的问题是:被消去的部分面积有多大?它的周长是多少?
分析 利用梯形的性质以及相似三角形的性质与判定分别得出△ADE的周长和面积即可.
解答 解:由题意可得:DE∥BC,
则△ADE∽△ABC,
故$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{{C}_{△ADE}}{{C}_{△ABC}}$,
∵AB的长由原来的30米缩短成BD长18米,
∴AD=12m,
即$\frac{12}{30}$=$\frac{{C}_{△ADE}}{{C}_{△ABC}}$=$\frac{{C}_{△ADE}}{80}$,
解得:C△ADE=32(m),
$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{2}{5}$)2=$\frac{4}{25}$=$\frac{{S}_{△ADE}}{100}$,
解得:S△ADE=16(m2).
点评 此题主要考查了相似三角形的应用,根题意得出△ADE∽△ABC求出相似比是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
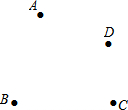 作图题.如图,在同一平面内有四个点A、B、C、D,
作图题.如图,在同一平面内有四个点A、B、C、D, 已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度) 小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.
小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.