题目内容
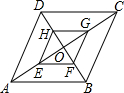 已知:如图,在菱形ABCD中,对角线AC与D相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,求证:四边形EFGH是菱形.
已知:如图,在菱形ABCD中,对角线AC与D相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,求证:四边形EFGH是菱形.考点:中点四边形
专题:证明题
分析:由菱形的性质结合三角形中位线定理,可得EF=FG=GH=HG,可证明四边形EFGH是菱形.
解答:证明:∵E、F为OA、OB的中点,
∴EF为△OAB的中位线,
∴EF=
AB,同理可得FG=
BC,GH=
CD,HE=
AD,
又∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形.
∴EF为△OAB的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形.
点评:本题主要考查菱形的性质和判定,掌握四边相等的四边形是菱形及三角形中位线定理是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
函数表达式y=
中的自变量x取值范围是( )
| 1 | ||
|
| A、x≥2 | B、x≤2 |
| C、x>2 | D、x<2 |
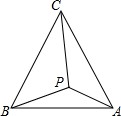 如图,P是等边△ABC内部的一点,PA=2,PB=2
如图,P是等边△ABC内部的一点,PA=2,PB=2 如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段的端点在格点上.
如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段的端点在格点上. 如图∠1与∠2是同位角,∠2与∠3是同位角,因此∠1与∠3是同位角,对吗?为什么?你是怎么来判断同位角的?
如图∠1与∠2是同位角,∠2与∠3是同位角,因此∠1与∠3是同位角,对吗?为什么?你是怎么来判断同位角的?