题目内容
若函数y=
与y=x-2图象的一个交点坐标(a,b),则
-
的值为 .
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据函数解析式,可得b=
,b=a-2,进而得出ab=1,b-a=-2,即可求得
-
=
=
=-2.
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
| -2 |
| 1 |
解答:解:∵函数y=
与y=x-2图象的一个交点坐标(a,b),
∴b=
,b=a-2,
∴ab=1,b-a=-2,
∴
-
=
=
=-2
故答案为-2.
| 1 |
| x |
∴b=
| 1 |
| a |
∴ab=1,b-a=-2,
∴
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
| -2 |
| 1 |
故答案为-2.
点评:本题考查了反比例函数一次函数的交点问题,根据函数解析式得到ab=1,b-a=-2是解决本题的关键..

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
点P(2,-1)在反比例函数y=
(k≠0)的图象上,则k的值是( )
| -k |
| x |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|




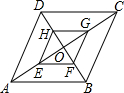 已知:如图,在菱形ABCD中,对角线AC与D相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,求证:四边形EFGH是菱形.
已知:如图,在菱形ABCD中,对角线AC与D相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,求证:四边形EFGH是菱形. 如图,∠B=30°,∠ACE=35°,CE平分∠ACB,求∠A的度数.
如图,∠B=30°,∠ACE=35°,CE平分∠ACB,求∠A的度数.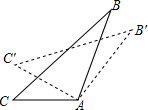 如图,△AB′C′是由△ABC绕顶点A按顺时针方向旋转后得到的,已知∠B=30°,∠C=40°.试探究:
如图,△AB′C′是由△ABC绕顶点A按顺时针方向旋转后得到的,已知∠B=30°,∠C=40°.试探究: 在所给平面直角坐标系中描点、画图:
在所给平面直角坐标系中描点、画图: 如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?
如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?