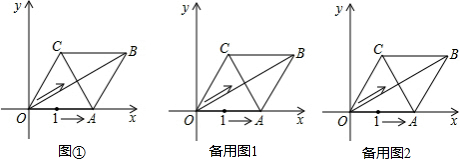
题目内容
如图，⊙
的半径
，四边形
内接圆⊙，
于点
，
为
延长线上的一点，且
.
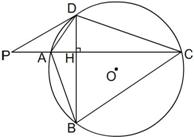（1）试判断
与⊙的位置关系，并说明理由：
（2）若
，
，求
的长；
（3）在（2）的条件下，求四边形的面积.
(1)如图，连接DO并延长交圆于点E，连接AE
∵DE是直径，∴∠DAE=90°，
∴∠E+∠ADE=90°
∵∠PDA=∠ADB=∠E
∴∠PDA+∠ADE=90°即PD⊥DO
∴PD与圆O相切于点D
(2) ∵tan∠ADB=
∴可设AH=3k,则DH=4k
∵
∴PA=
∴PH=
∴∠P=30°，∠PDH=60°
∴∠BDE=30°
连接BE，则∠DBE=90°，DE=2r=50
∴BD=DE·cos30°=
(3)由（2）知，BH=-4k，∴HC=
(-4k)
又∵
∴
解得k=
∴AC=
∴S=
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
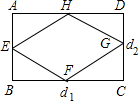已知⊙O1和⊙O2的半径分别是8.5cm和3.5cm，当两圆外切时圆心距为d1，两圆内切时圆心距为d2，如图，以d1和d2长为邻边作矩形ABCD，依次连接矩形ABCD四边中点，得四边形EFGH，则四边形EFGH周长是
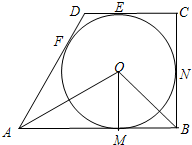（2012•五通桥区模拟）如图，梯形ABCD，AB∥CD，AB=2cm，梯形ABCD内部的⊙O分别切四边于E，F，M，N，且∠OAB=30°，∠OBA=45°．
