Question

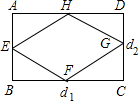已知⊙O₁和⊙O₂的半径分别是8.5cm和3.5cm，当两圆外切时圆心距为d₁，两圆内切时圆心距为d₂，如图，以d₁和d₂长为邻边作矩形ABCD，依次连接矩形ABCD四边中点，得四边形EFGH，则四边形EFGH周长是

 

cm．

Answer 1

分析：根据两圆的位置关系和数量之间的联系，分别求得矩形的长和宽，再根据勾股定理求得矩形的对角线的长，进而根据三角形的中位线定理求得四边形的边长，最后可求得其周长．

解答：解：根据题意，得
d₁=8.5+3.5=12cm，d₂=8.5-3.5=5cm，
故AD=BC=12cm，AB=CD=5cm；
连接AC，BD，
由勾股定理，得AC=

AD2+CD2

=

122+52

=13，
同理可得BD=13，
由三角形的中位线定理，得
EH=GF=

1

2

BD=

1

2

×13=

13

2

；EF=HG=

1

2

AC=

1

2

×13=

13

2

．
则四边形EFGH周长是=4EF=4×

13

2

=26（cm）．

点评：本题考查的是圆与圆的位置关系与数量之间的联系及三角形的中位线定理．