题目内容
7. 如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,⊙O的直径PC⊥AB,连接PA、PB.若sin∠BAC=$\frac{4}{5}$,则tan∠PAB=$\frac{3}{4}$.
如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,⊙O的直径PC⊥AB,连接PA、PB.若sin∠BAC=$\frac{4}{5}$,则tan∠PAB=$\frac{3}{4}$.
分析 先根据垂径定理得出$\widehat{AP}$=$\widehat{PB}$,故∠PAB=∠PBA=∠ACP,再由圆周角定理得出∠PAC=90°,由sin∠BAC=$\frac{4}{5}$可设CD=4x,则AC=5x,由勾股定理可知AD=3x,故tan∠ACP=$\frac{AD}{CD}$=$\frac{3x}{4x}$=$\frac{3}{4}$,由此可得出结论.
解答 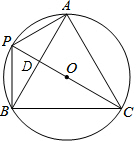 解:∵⊙O的直径PC⊥AB,
解:∵⊙O的直径PC⊥AB,
∴$\widehat{AP}$=$\widehat{PB}$,
∴∠PAB=∠PBA=∠ACP.
∵PC是⊙O的直径,
∴∠PAC=90°.
∵sin∠BAC=$\frac{4}{5}$,
∴设CD=4x,则AC=5x,由勾股定理可知AD=3x,
∴tan∠ACP=$\frac{AD}{CD}$=$\frac{3x}{4x}$=$\frac{3}{4}$,即tan∠PAB=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列方程是一元二次方程的是( )
| A. | 3x+1=5x+7 | B. | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C. | ax2-bx=5(a和b为常数) | D. | m2-2m=3 |
17.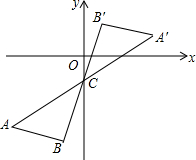 如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )
如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )
 如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )
如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n+2) | D. | (-m,-n-4) |
 如图,已知直线y=-2x+8和x轴、y轴分别交于B和A,直线l经过点C(2,-4)和D(0,-3),向下平移1个单位后与x轴、y轴分别交于点E、F,直线AB和EF相交于点P.
如图,已知直线y=-2x+8和x轴、y轴分别交于B和A,直线l经过点C(2,-4)和D(0,-3),向下平移1个单位后与x轴、y轴分别交于点E、F,直线AB和EF相交于点P.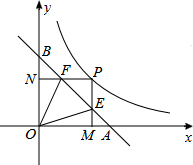 如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=$\frac{k}{x}$(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为$\frac{1}{2}$.
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=$\frac{k}{x}$(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为$\frac{1}{2}$.