题目内容
19.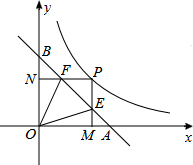 如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=$\frac{k}{x}$(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为$\frac{1}{2}$.
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=$\frac{k}{x}$(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为$\frac{1}{2}$.
分析 首先设P(a,b),由直线y=-x+1分别交x轴、y轴于A,B两点,可得△AOB为等腰直角三角形,由E和F都在直线y=-x+1上,可求得BE=$\sqrt{2}$a,AF=$\sqrt{2}$b,又易证得△AOF∽△BEO,根据相似三角形的性质即可得k的值.
解答 解:设P(a,b),则OM=a,PM=b,则点E的横坐标为a,F的纵坐标为b,
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=$\sqrt{{a}^{2}+(1-1+a)^{2}}$=$\sqrt{2}$a,AF=$\sqrt{(1-1-b)^{2}+{b}^{2}}$=$\sqrt{2}$b,
∵∠EOF=45°,
∴△AOF∽△BEO,
∴AF:BO=AO:BE,
∴AF•BE=BO•AO,
即$\sqrt{2}$a•$\sqrt{2}$b=1×1,
解得ab=$\frac{1}{2}$,
∴反比例函数y=$\frac{k}{x}$(x>0)中k的值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了反比例函数综合题,涉及的知识点有:等腰直角三角形的性质、相似三角形的判定与性质以及点与函数的关系.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
9. 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )| A. | 1条 | B. | 4条 | C. | 8条 | D. | 10条 |
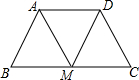 如图,已知AD∥BC,M是BC的中点,且MA=MD,求证:△ABM≌△DCM.
如图,已知AD∥BC,M是BC的中点,且MA=MD,求证:△ABM≌△DCM. 如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,⊙O的直径PC⊥AB,连接PA、PB.若sin∠BAC=$\frac{4}{5}$,则tan∠PAB=$\frac{3}{4}$.
如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,⊙O的直径PC⊥AB,连接PA、PB.若sin∠BAC=$\frac{4}{5}$,则tan∠PAB=$\frac{3}{4}$. 如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$.
如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$. 在已给图形的基础上画图,使之成为图形,并且满足第一幅图只有一条对称轴,第二幅图只有两条对称轴.
在已给图形的基础上画图,使之成为图形,并且满足第一幅图只有一条对称轴,第二幅图只有两条对称轴.