请你写出一个二元一次方程组:$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$.使它的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．题目和参考答案——青夏教育精英家教网—

题目内容

6．请你写出一个二元一次方程组：$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$，使它的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．

分析由1与2列出两个算式，即可确定出所求方程组．

解答解：根据题意得：$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$．

点评此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

练习册系列答案

相关题目

11．

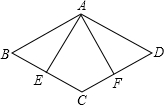在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，则∠EAF等于（　　）

17．若a＜0，b＞0，则化简$\sqrt{{a}^{2}{b}^{3}}$的结果为（　　）

14．

如图，在平面直角坐标系中，⊙P的圆心坐标是（4，a）（a＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{15}$，则⊙P的弦心距是1；a的值是4+$\sqrt{2}$．

1．已知方程组$\left\{\begin{array}{l}{k{x}^{2}-x-y+1/2=0}\\{y=k（2x-1）}\end{array}$ （x、y为未知数）有两个不同的实数解$\left\{\begin{array}{l}{x={x}_{1}}\\{y={y}_{1}}\end{array}$或$\left\{\begin{array}{l}{x={x}_{2}}\\{y={y}_{2}}\end{array}\right.$．
（1）求实数k的取值范围；
（2）如果y₁y₂+$\frac{1}{x_1}+\frac{1}{x_2}$=3，求实数k的值．

11．如图1，正方形ABCD，△AMN是等腰Rt△，∠AMN=90°，当Rt△AMN绕点A旋转时，边AM、AN分别与BC（或延长线图3）、CD（或延长线图3）相交于点E、F，连接EF，小明与小红在研究图1时，发现有这么一个结论：EF=DF+BE；为了解决这个问题，小明与小红，经过讨论，采取了以下方案：延长CB到G，使BG=DF，连接AG，得到图2，请你根据小明、小红的思路，结合图2，解决下列问题：
（1）证明：△ADF≌△ABG；
（2）根据图（3），①结论EF=DF+BE是否成立，如不成立，写出三线段EF、DF、BE的数量关系并证明．
②若CE=6，DF=2，求：正方形ABCD的边长以及△AEF中AE边上的高．

18．若-2a^mb⁴与5a²bⁿ⁺⁷是同类项，则mⁿ=$\frac{1}{8}$．

15．计算3y³•（-y²）²•（-2y）³的结果是（　　）

-24y¹⁰

-6y¹⁰

-18y¹⁰

54y¹⁰

16．求不等式组-5≤3x+1＜x+7的整数解．

试题分类