题目内容
8. 如图所示,△ABC为直角三角形,∠A=30°,
如图所示,△ABC为直角三角形,∠A=30°,(1)求cosA-$\sqrt{3}$cosB+$\sqrt{2}$sin45°;
(2)若AB=4,求△ABC的面积.
分析 将特殊角的三角函数值代入求解即可.
解答 解:(1)因为△ABC为直角三角形,∠A=30°,
所以B=60°,
$cosA=\frac{{\sqrt{3}}}{2}$,$cosB=\frac{1}{2}$,$sin{45°}=\frac{{\sqrt{2}}}{2}$,
$cosA-\sqrt{3}cosB+\sqrt{2}sin{45°}$
=$\frac{{\sqrt{3}}}{2}-\sqrt{3}•\frac{1}{2}+\sqrt{2}•\frac{{\sqrt{2}}}{2}$
=1
(2)若AB=4,则$BC=AB•sin{30°}=4×\frac{1}{2}=2$
$AC=AB•cos{30°}=4×\frac{{\sqrt{3}}}{2}=2\sqrt{3}$
所以 ${S_{△ABC}}=\frac{1}{2}•AC•BC=\frac{1}{2}×2\sqrt{3}×2=2\sqrt{3}$
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
相关题目
3.等式$\sqrt{x+1}$•$\sqrt{x-1}$=$\sqrt{{x}^{2}-1}$成立的条件是( )
| A. | x≥1 | B. | x≥-1 | C. | -1≤x≤1 | D. | x≥1或x≥-1 |
13.下列说法正确的是( )
| A. | 绝对值等于它本身的数是正数 | B. | 经过三个点一定可以画三条直线 | ||
| C. | 若a2=b2,则a=b | D. | 整数和分数统称为有理数 |
17.下列四个图形中,是中心对称图形的是( )
| A. |  等腰梯形 | B. |  正三角形 | C. |  | D. |  正五边形 |
18.已知a=2017x+2016,b=2017x+2017,c=2017x+2018,那么a2+b2+c2-ab-bc-ca的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
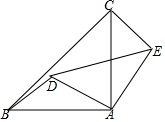 如图,△ABC和△ADE都是等腰直角三角形.
如图,△ABC和△ADE都是等腰直角三角形. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正确结论的序号是①③④.
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正确结论的序号是①③④.