题目内容
9.在Rt△ABC中,∠C=90°,中线AD,CE相交于G,且CG=3,则AB=9.分析 根据重心的概念得到点G是△ABC的重心,根据重心的性质求出GE,得到CE,根据在直角三角形中,斜边上的中线等于斜边的一半解答即可.
解答 解: ∵中线AD,CE相交于G,
∵中线AD,CE相交于G,
∴点G是△ABC的重心,
∴GE=$\frac{1}{2}$CG=1.5,
∴CE=CG+GE=4.5,
∵∠C=90°,CE是中线,
∴AB=2CE=9.
故答案为:9.
点评 本题考查的是三角形的重心的概念和性质、直角三角形的性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍,在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
17.一列火车长150m,以15m/s的速度通过600m的隧道,从火车进入隧道口算起,到这列火车完全通过隧道所需时间是( )
| A. | 30s | B. | 40s | C. | 50s | D. | 60s |
14.下列计算正确的是( )
| A. | a3-a2=a | B. | -2(a+b)=-2a-b | C. | -4a-(-9a)=-5a | D. | -2(a-b)=-2a+2b |
18.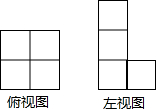 如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )
如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )
 如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )
如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )| A. | 5或6或7 | B. | 6或7 | C. | 7或8 | D. | 6或7或8 |
 如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为12.
如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为12. 如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,