题目内容
19．
如图，△ABC中，CD⊥AB于D，E是AC的中点，若AD=9，DE=7.5，则CD的长为12．
分析 利用直角三角形的性质得出AC的长，再利用勾股定理得出DC的长．
解答 解：∵CD⊥AB于D，E是AC的中点，
∴DE=AE=EC，
∵AD=9，DE=7.5，
∴AC=15，
∴在Rt△ADC中
AD2+DC2=AC2，
即DC2=AC2-AD2=225-81=144，
故DC=12．
故答案为：12．
点评 此题主要考查了直角三角形的性质以及勾股定理，得出AC的长是解题关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
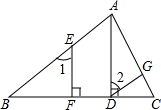如图，已知AD⊥BC，EF⊥BC，∠1=∠2．求证：DG∥BA．
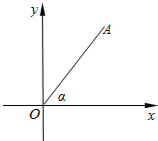如图，点A（t，4）在第一象限，OA与x轴所夹的锐角为α，sinα=$\frac{2}{3}$，求t的值．
如图所示，先将图沿着它自己的右边缘翻折，再绕着右下角的一个端点按顺时针方向旋转180°，之后所得到的图形是（ ）
如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E，若AB=6，求线段DE的长．
11．下列计算正确的是（ ）
| A． | x2•x3=x5 | B． | x2+x3=2x5 | C． | 2x-3x=-1 | D． | （2x）3=2x3 |
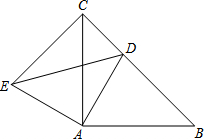已知：如图，等腰△ABC，AB=AC，点D为△ABC的BC边上一点，连接AD，将线段AD旋转至AE，使得∠DAE=∠BAC，连接CE．