题目内容
已知三个实数a、b、c满足a+b+c=0,abc=1,求证:a、b、c中至少有一个大于 •
•
证明:∵a+b+c=0,
∴a、b、c必有一个正数,
不妨设c>0,a+b=-c,ab= .
.
这样a、b可看作方程x2+cx+ =0的两实根.
=0的两实根.
△=c2-4× ≥0,即c3≥4>
≥0,即c3≥4>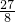 ,∴c>
,∴c> =
= .
.
所以a、b、c中至少有一个大于 •
•
分析:由a+b+c=0,得到三个实数a、b、c中比有一个正数;不妨设c>0,这样用c表示a+b和ab,然后写出以a,b为根的一元二次方程,由△≥0得到c的范围,最后经过数的变换,确定c大于 .
.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了根与系数的关系.
∴a、b、c必有一个正数,
不妨设c>0,a+b=-c,ab=
 .
.这样a、b可看作方程x2+cx+
 =0的两实根.
=0的两实根.△=c2-4×
 ≥0,即c3≥4>
≥0,即c3≥4>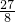 ,∴c>
,∴c> =
= .
.所以a、b、c中至少有一个大于
 •
•分析:由a+b+c=0,得到三个实数a、b、c中比有一个正数;不妨设c>0,这样用c表示a+b和ab,然后写出以a,b为根的一元二次方程,由△≥0得到c的范围,最后经过数的变换,确定c大于
 .
.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了根与系数的关系.

练习册系列答案
相关题目
已知三个实数a,b,c中,其中一个是另两个的比例中项,若a=1,b=2,则满足条件的c的取值有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
已知三个实数x1,x2,x3,它们中任何一个数加其余两个数的积的5倍总等于6,这样的三元数组(x1,x2,x3),共有( )
| A、2组 | B、3组 | C、4组 | D、5组 |