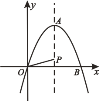题目内容
【题目】问题发现
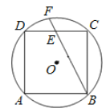
(1)如图1,![]() 和
和![]() 均为等边三角形,点D在边BC上,连接CE.求证:
均为等边三角形,点D在边BC上,连接CE.求证:![]() .
.
拓展探究
(2)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点D在边BC上,连接CE
,点D在边BC上,连接CE
ⅰ)求![]() 的度数;
的度数;
ⅱ)请判断线段AC、CD、CE之间的数量关系,并说明理由.
解决问题
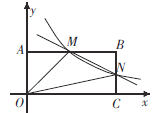
(3)如图3,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,AC与BD交于点E,求出线段AC的长度.
,AC与BD交于点E,求出线段AC的长度.

【答案】(1)见解析;(2)i)![]() ,ⅱ)
,ⅱ)![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)根据SAS可证明△BAD≌△CAE,可得结论;
(2)i)先证明△ABD≌△ACE,得∠ACE=∠B=45°;
ⅱ)由△ABD≌△ACE,得BD=CE,利用等边三角形的AC=BC=BD+DC等量代换可得结论;
(3)过点A作AC的垂线,交CB的延长线于点F,证明△ACF是等腰直角三角形,则利用(2)的结论求AC的长.
(1)∵![]() 和
和![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)i)![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
ⅱ)![]() ;
;
理由:由ⅰ)得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵在等腰![]() 中,
中,![]() ,
,
∴![]() ;
;
(3)如解图,过点A作AC的垂线,交CB的延长线于点F,
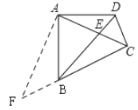
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴A、B、C、D四点共圆,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
由(2)得![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)