题目内容
2.符号“f”表示一种运算,它对一些数的运算如下:$f(1)=1+\frac{2}{1}$,$f(2)=1+\frac{2}{2}$,$f(3)=1+\frac{2}{3}$,…,利用以上运算的规律写出f(n)=1+$\frac{2}{n}$(n为正整数);f(1)•f(2)•f(3)…f(99)=$\frac{101}{3}$.分析 根据已知等式归纳总结得到一般性规律,写出即可;原式利用新定义化简,约分即可得到结果.
解答 解:根据题意得:f(n)=1+$\frac{2}{n}$(n为正整数);
f(1)•f(3)•f(5)f(7)…f(99)=(1+2)×(1+$\frac{2}{3}$)×(1+$\frac{2}{5}$)×…×(1+$\frac{2}{99}$)=3×$\frac{5}{3}$×$\frac{7}{5}$×…×$\frac{101}{99}$=$\frac{101}{3}$.
故答案为:1+$\frac{2}{n}$;$\frac{101}{3}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.下面是某同学在一次数学检验中解答的填空题,其中答对的是( )
| A. | 若x2=4,则x=2 | B. | x2+x+k=0的一个根是1,则k=2 | ||
| C. | 若x2=x,则x=1 | D. | 若分式$\frac{x(x-2)}{x}$的值为零,则x=2 |
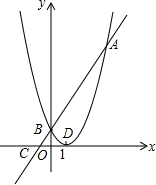 如图,已知抛物线y=(x-1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D,
如图,已知抛物线y=(x-1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D, 如图,已知⊙0的半径为5,C是弦AB的中点,OC=3,求弦AB的长.
如图,已知⊙0的半径为5,C是弦AB的中点,OC=3,求弦AB的长.