题目内容
2.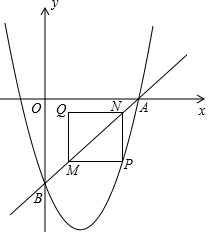 如图,直线y=2x-6与抛物线y=2x2+bx+c相交于A,B两点,点A在x轴上,点B在y轴上,点P在直线AB下方的抛物线上,过P点分别作PM∥x轴交AB于M点,PN∥y轴交AB于N点,以PM、PN为边作矩形PMQN,设点Q的坐标为(m,n).
如图,直线y=2x-6与抛物线y=2x2+bx+c相交于A,B两点,点A在x轴上,点B在y轴上,点P在直线AB下方的抛物线上,过P点分别作PM∥x轴交AB于M点,PN∥y轴交AB于N点,以PM、PN为边作矩形PMQN,设点Q的坐标为(m,n).(1)求b,c的值;
(2)求m与n的函数关系式;
(3)确定点P的位置,使矩形PMQN的周长最大,并求出这个最大值.
分析 (1)先求得点A、B的坐标,然后将点A、B的坐标代入抛物线的解析式得到关于b,c的方程组,解方程组可得到b,c的值;
(2)先得到抛物线的解析式,设P(a,2a2-4a-6),则N(a,2a-6),M(m,2m-6),然后依据与坐标轴平行的直线上点的坐标特点可得到n=2a-6①,2m-6=2a2-4a-6②,然后消去字母a可得到m与n之间的函数关系式;
(3)依据题意可知PM=$\frac{1}{2}$PN,则矩形QMPN的周长=3PN.设P(a,2a2-4a-6),则N(a,2a-6),然后得到PN与a的函数关系式,最后利用二次函数的性质求解即可.
解答 解:(1)将x=0代入y=2x-6得y=-6,则B(0,-6).
将y=0代入y=2x-6得:2x-6=0,解得:x=3,则A(3,0).
将点B和点A的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{18+3b+c=0}\\{c=-6}\end{array}\right.$,
解得:b=-4,c=-6.
(2)∵b=-4,c=-6,
∴抛物线的解析式为y=2x2-4x-6.
设P(a,2a2-4a-6),则N(a,2a-6).
∵Q(m,n),
∴M(m,2m-6).
∵PN∥MQ,QA∥MP,
∴n=2a-6①,2m-6=2a2-4a-6②.
由①得:a=$\frac{n+6}{2}$③,m=a2-2a④.
将③代入④得:m=$\frac{1}{4}$n2+2n+3.
(3)∵A(3,0),B(0,-6),
∴OA=3,OB=6.
∴tan∠OBA=$\frac{1}{2}$.
∵PN∥OB,
∴tan∠PNM=$\frac{PM}{PN}$=$\frac{1}{2}$.
∴PM=$\frac{1}{2}$PN.
∴矩形QMPN的周长=2×(PM+PN)=2×$\frac{3}{2}$PN=3PN.
设P(a,2a2-4a-6),则N(a,2a-6),PN=2a-6-(2a2-4a-6)=-2(a-$\frac{3}{2}$)2+$\frac{9}{2}$.
∴当a=$\frac{3}{2}$时,矩形的周长最大.
∴P($\frac{3}{2}$,-$\frac{15}{2}$).
∴矩形的最大周长=3×$\frac{9}{2}$=$\frac{27}{2}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义,二次函数的性质得到PN与a的函数关系式是解题的关键.

| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 19 | 13 | 13 |

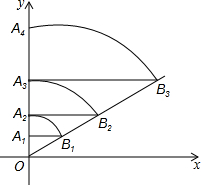 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).