题目内容
14.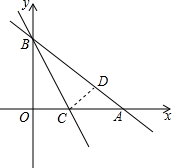 如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3).
如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3).(1)求一次函数解析式;
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D点处,求直线BC的表达式;
(3)是否存在x轴上一个动点P,使△ABP为等腰三角形?若存在请直接写出P点坐标;若不存在,请说明理由.
分析 (1)先设一次函数的解析式为y=kx+b(k≠0),利用待定系数法将点A、B的坐标代入一次函数解析式即可求得k与b的值,从而得到解析式;
(2)利用翻折性质及勾股定理求出点C的坐标,再利用待定系数法求出直线BC的解析式;
(3)分别利用当AB=P1B时,当AB=AP2时,当P3A=P3B时,当AB=AP4时,求出点P的坐标即可.
解答 解:(1)设一次函数的表达式为y=kx+b,
∵A、B两点的坐标分别为(4,0),(0,3).
∴$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,
解得k=-$\frac{3}{4}$,
∴y=-$\frac{3}{4}$x+3;
(2)由题意得OA=4,OB=3,∴AB=5,
由翻折可得OC=CD,BD=BO=3,∴AD=2.
设CD=OC=x,则AC=OA-OC=4-x.
在Rt△ACD中,由勾股定理得:CD2+AD2=AC2,
即:x2+22=(4-x)2
解得:x=$\frac{3}{2}$.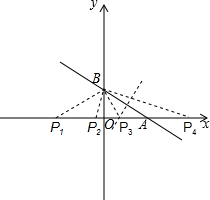
∴C的坐标为($\frac{3}{2}$,0).
设直线BC的解析式为y=mx+n,
将点B(0,3)、C($\frac{3}{2}$,0)代入得:$\left\{\begin{array}{l}{n=3}\\{m+n=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{n=3}\\{m=-2}\end{array}\right.$
∴直线BC的解析式为:y=-2x+3.
(3)当AB=P1B时,∵AO=4,∴OP1=AO=4,故点P1(-4,O),
当AB=AP2时,∵BO=3,AO=4,∴AB=5,则OP2=AB-AO=1,则点P2(-1,0)
当P3A=P3B时,∵BO=3,AO=4,∴AB=5,
设OP3=x,则BP3=4-x,故32+x2=(4-x)2,
解得:x=$\frac{7}{8}$,
故点P3($\frac{7}{8}$,0)
当AB=AP4时,∵BO=3,AO=4,∴AB=5,则AP4=AB=5,故点P4(9,0),
综上所述:P点坐标为:(-4,0),(-1,0),(9,0),($\frac{7}{8}$,0).
点评 本题主要考查了等腰三角形性质,待定系数法求一次函数解析式以及一次函数的综合应用,要注意的是(3)中,要根据P点的不同位置进行分类求解.

 星级口算天天练系列答案
星级口算天天练系列答案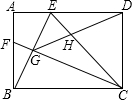 如图,在矩形ABCD中,E是AD边上的一点,CF垂直平分BE于点G,交AB于点F,连接DG、CE交于点H.若DE=2AE,则给出下列结论:①DG=CG;②3AF=2BF;③DG平分∠EGC;④EH=$\frac{{\sqrt{30}}}{10}$HD.其中正确的结论是( )
如图,在矩形ABCD中,E是AD边上的一点,CF垂直平分BE于点G,交AB于点F,连接DG、CE交于点H.若DE=2AE,则给出下列结论:①DG=CG;②3AF=2BF;③DG平分∠EGC;④EH=$\frac{{\sqrt{30}}}{10}$HD.其中正确的结论是( )| A. | 只有①② | B. | 只有①②④ | C. | 只有③④ | D. | ①②③④ |
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 不是有理数 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,则BD=$\frac{9}{5}$.
如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,则BD=$\frac{9}{5}$.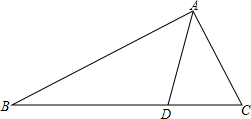 如图,在△ABC中,AD平分∠BAC,∠C=2∠B,
如图,在△ABC中,AD平分∠BAC,∠C=2∠B,