题目内容
6.将正方形A的一个顶点与正方形B的对角线交点重合,如图(1),则阴影部分面积是正方形A的面积的$\frac{1}{8}$,若将正方形B的一个顶点与正方形A的对角线交点重合,按图(2),则阴影部分面积是正方形B面积的( )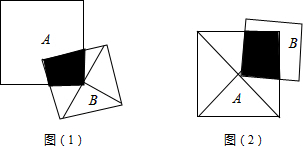
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 设正方形B的面积为S,正方形B对角线的交点为O,标注字母并过点O作边的垂线,根据正方形的性质可得OE=OM,∠EOM=90°,再根据同角的余角相等求出∠EOF=∠MON,然后利用“角边角”证明△OEF和△OMN全等,根据全等三角形的面积相等可得阴影部分的面积等于正方形B的面积的$\frac{1}{4}$,再求出正方形A的面积,同理可得图(2)中的阴影部分的面积等于正方形A的面积的$\frac{1}{4}$,然后整理即可得解.
解答 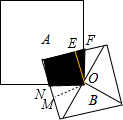 解:如图,设正方形B的面积为S,正方形B对角线的交点为O,
解:如图,设正方形B的面积为S,正方形B对角线的交点为O,
过点O作边的垂线,则OE=OM,∠EOM=90°,
∵∠EOF+∠EON=90°,∠MON+∠EON=90°,
∴∠EOF=∠MON,
在△OEF和△OMN中,$\left\{\begin{array}{l}{∠EOF=∠MON}\\{OE=OM}\\{∠OEF=∠OMN=90°}\end{array}\right.$,
∴△OEF≌△OMN(ASA),
∴阴影部分的面积=$\frac{1}{4}$S,
∵阴影部分面积是正方形A面积的$\frac{1}{8}$,
∴$\frac{1}{4}$S=$\frac{1}{8}$SA,
∴SA=2S,
同理可得,图(2)中阴影部分的面积=$\frac{1}{4}$SA,
∴阴影部分的面积=$\frac{1}{4}$×2S=$\frac{1}{2}$S,
∴阴影部分面积是正方形B面积的$\frac{1}{2}$.
故选:C.
点评 本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
18.下列四个图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
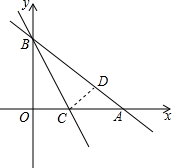 如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3).
如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3). 如图,沿图中的右边缘所在的直线为轴将该图形向右翻折180°后,再将翻折后的正方形绕它的右下顶点按顺时针方向旋转90°,所得到的图形是( )
如图,沿图中的右边缘所在的直线为轴将该图形向右翻折180°后,再将翻折后的正方形绕它的右下顶点按顺时针方向旋转90°,所得到的图形是( )



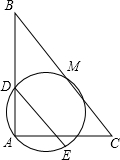 已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.
已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.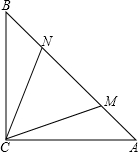 如图,△ABC为等腰直角三角形,∠ACB=90°,M,N为斜边A,B上两点,且满足BN2+AM2=MN2,则∠MCN=45°.
如图,△ABC为等腰直角三角形,∠ACB=90°,M,N为斜边A,B上两点,且满足BN2+AM2=MN2,则∠MCN=45°.