题目内容

11．如图，正方形ABCD的面积为5，点M，N，P分别是边BC，CD和对角线BD上的动点，则PM+PN的最小值为$\sqrt{5}$．

分析 在AB上取BN′=BN，连结PN′，先证明△PNB≌PN′B，则NP=PN′，然后将MP+PN转化为PM+PN′，当点N、P、M在一条直线上且MN⊥DC时，MP+PN有最小值，最小值等于正方形的边长．

解答 解：在AB上取BN′=BN，连结PN′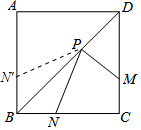

∵ABCD为正方形，
∴∠ABD=∠CBD=45°．
在△PNB和PN′B中$\left\{\begin{array}{l}{BN′=NB}\\{∠NBP=∠N′BP}\\{BP=BP}\end{array}\right.$，
∴△PNB≌PN′B．
∴NP=PN′．
∴MP+PN=PM+PN′．
当点N、P、M在一条直线上且MN⊥DC时，MP+PN有最小值，最小值等于正方形的边长=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题主要考查的是轴对称路径最短、正方形的性质、垂线段的性质，熟练将将MP+PN转化为PM+PN′是解题的关键．

练习册系列答案
相关题目
1．计算或化简：
（1）$\frac{2}{3}$$\sqrt{18}$÷（-$\sqrt{3}}$）×$\frac{1}{3}$$\sqrt{27}$
（2）（$\frac{x+8}{{{x^2}-4}}$-$\frac{2}{x-2}}$）÷$\frac{x-4}{{{x^2}-4x+4}}$．
2．问题情境：
两张矩形纸片ABCD和CEFG完全相同，且AB=CE，AD＞AB．
操作发现：
（1）如图1，点D在GC上，连接AC、CF、CG、AG，则AC和CF有何数量关系和位置关系？并说明理由．
实践探究：
（2）如图2，将图1中的纸片CEFG以点C为旋转中心逆时针旋转，当点D落在GE上时停止旋转，则AG和GF在同一条直线上吗？请判断，并说明理由．
19．（1）计算：$\sqrt{8}$+（-2017）0-4sin45°
（2）化简：m（1-m）+（m-2）2．
6．如图，平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且满足|a+2|+$\sqrt{b-3}$=0，现同时将点A，B分别向上平移4个单位长度，再向右平移2个单位长度，分别得到点A，B的对应点D，C，连接AD，BC，CD．
（1）求点C，D的坐标及四边形ABDC的面积．
（2）在y轴上是否存在一点P，使三角形PAB的面积等于四边形ABCD的面积？若存在，请求出点P的坐标；若不存在，请说明理由．
（3）点E是线段BC上一个动点，连接DE，OE，当点E在BC上移动时（不与点B，C重合）$\frac{∠CDE+∠BOE}{∠OED}$的值是否发生变化？并说明理由．
16．如图，在平面直角坐标系中，点A是反比例函数y=$\frac{k}{x}$（x＜0）的图象上一点，过点A作AB⊥x轴，垂足为B，点C是y轴上任意一点，连接AC、BC，若△ABC的面积为2，则k的值为-4．
3．如图，在?ABCD中，AC、BD相交于点O，点E是AB的中点．若OE=1cm，则AD的长是（　　）cm．
A．2B．3C．4D．5
20．为响应“足球进校园”的号召，某校到商场购买甲、乙两种足球，购买甲种足球共花费1600元，乙种足球共花费1200元．已知甲种足球的单价是乙种足球单价的2倍，且购买甲种足球的数量比乙种足球少10个．
（1）设乙种足球的单价为x元，用含x的代数式表示下表中相关的量
 品种购买个数 单价 总价 
甲种足球 $\frac{1200}{x}$-10 2x1600
 乙种足球$\frac{1200}{x}$ x 1200 
（2）列方程求乙种足球的单价．
15．若（a-b）2+2（a-b）+1=0，则（a-b）2013等于（　　）
A．2013B．-1C．0D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网