题目内容
6.如图,平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且满足|a+2|+$\sqrt{b-3}$=0,现同时将点A,B分别向上平移4个单位长度,再向右平移2个单位长度,分别得到点A,B的对应点D,C,连接AD,BC,CD.(1)求点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,使三角形PAB的面积等于四边形ABCD的面积?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点E是线段BC上一个动点,连接DE,OE,当点E在BC上移动时(不与点B,C重合)$\frac{∠CDE+∠BOE}{∠OED}$的值是否发生变化?并说明理由.

分析 (1)根据非负数的性质求出a、b的值,根据平移的性质、平行四边形的面积公式解答;
(2)设点P的坐标为(0,y),根据三角形的面积公式列出算式,计算即可;
(3)作EF∥AB交OD于F,根据平行线的性质解答.
解答 解:(1)∵|a+2|+$\sqrt{b-3}$=0,
∴a+2=0,b-3=0,
解得,a=-2,b=3,
则点A,B的坐标分别为A(-2,0),B(3,0),
由题意得,点C,D的坐标分别为(5,4),(0,4),
∴四边形ABDC的面积=5×4=20;
(2)设点P的坐标为(0,y),
则$\frac{1}{2}$×AB×|y|=20,
解得,y=±8,
∴点P的坐标为(0,8)或(0,-8)时,三角形PAB的面积等于四边形ABCD的面积;
(3)不变.
作EF∥AB交OD于F,
∵CD∥AB,
∴EF∥CD,
∴∠CDE=∠DEF,∠BOE=∠OEF,
∴∠CDE+∠BOE=∠DEO,
∴$\frac{∠CDE+∠BOE}{∠OED}$=1.
点评 本题考查的是平行四边形的性质、非负数的性质,掌握平行四边形的对边平行、平行线的性质是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.
如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm. 在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点.
在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点.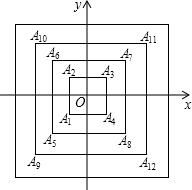 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A51的坐标是(13,13).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A51的坐标是(13,13). 如图,正方形ABCD的面积为5,点M,N,P分别是边BC,CD和对角线BD上的动点,则PM+PN的最小值为$\sqrt{5}$.
如图,正方形ABCD的面积为5,点M,N,P分别是边BC,CD和对角线BD上的动点,则PM+PN的最小值为$\sqrt{5}$. 在图中,利用网格点和三角板画图或计算:
在图中,利用网格点和三角板画图或计算: