题目内容
13.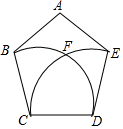 如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则$\widehat{BF}$的长为$\frac{8}{15}$π.
如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则$\widehat{BF}$的长为$\frac{8}{15}$π.
分析 连接CF,DF,得到△CFD是等边三角形,得到∠FCD=60°,根据正五边形的内角和得到∠BCD=108°,求得∠BCF=48°,根据弧长公式即可得到结论.
解答  解:连接CF,DF,
解:连接CF,DF,
则△CFD是等边三角形,
∴∠FCD=60°,
∵在正五边形ABCDE中,∠BCD=108°,
∴∠BCF=48°,
∴$\widehat{BF}$的长=$\frac{48•π×2}{180}$=$\frac{8}{15}$π,
故答案为:$\frac{8}{15}$π.
点评 本题考查了正多边形与圆,弧长的计算,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
3.-|-125|的立方根是( )
| A. | -$\frac{25}{3}$ | B. | $\frac{25}{3}$ | C. | 5 | D. | -5 |
4.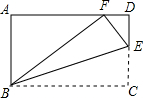 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{5}{3}$ |
1.在平面直角坐标系中,点P(-2,$\sqrt{3}$)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.将不等式x-1>0的解集表示在数轴上,下列表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
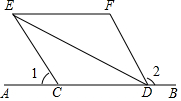 已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.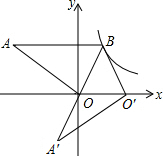 如图,△AOB,AB∥x轴,OB=2,点B在反比例函数y=$\frac{k}{x}$上,将△AOB绕点B逆时针旋转,当点O的对应点O′落在x轴的正半轴上时,AB的对应边A′B恰好经过点O,则k的值为$\sqrt{3}$.
如图,△AOB,AB∥x轴,OB=2,点B在反比例函数y=$\frac{k}{x}$上,将△AOB绕点B逆时针旋转,当点O的对应点O′落在x轴的正半轴上时,AB的对应边A′B恰好经过点O,则k的值为$\sqrt{3}$.
 解不等式组:$\left\{\begin{array}{l}1-3(x-1)<8-x\\ \frac{x-3}{2}+3≥x+1\end{array}\right.$,再写出它的整数解.
解不等式组:$\left\{\begin{array}{l}1-3(x-1)<8-x\\ \frac{x-3}{2}+3≥x+1\end{array}\right.$,再写出它的整数解.