题目内容
18．先化简，再求值：（2x2y-4xy2）÷（x2-y2），其中：（x+2）2+$\sqrt{y-1}$=0．分析 首先化简整式进而利用绝对值和二次根式的性质化简得出x，y的值代入求出即可．
解答 解：（2x2y-4xy2）÷（x2-y2）
=2xy（x-2y）÷（x+y）（x-y）
∵（x+2）2+$\sqrt{y-1}$=0，
∴$\left\{\begin{array}{l}{x+2=0}\\{y-1=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$，
故原式=2xy（x-2y）÷（x+y）（x-y）
=2×（-2）×1（-2-2）÷（-2+1）（-2-1）
=$\frac{16}{3}$．
点评 此题主要考查了整式的混合运算以及非负数的性质，得出x，y的值是解题关键．
练习册系列答案
53随堂测系列答案
相关题目
8．某小区超市一段时间每天订购80个面包进行销售，每售出1个面包获利润0.5元，未售出的每个亏损0.3元．（1）若今后每天售出的面包个数用x（0＜x≤80）表示，每天销售面包的利润用y（元）表示，写出y与x的函数关系式；
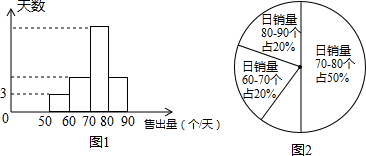
（2）小明连续m天对该超市的面包销量进行统计，并制成了频数分别直方图（每个组距包含左边的数，但不包含右边的数）和扇形统计图，如图1、图2所示，请结合两图提供的信息，解答下列问题：
①m的值为30；
②求在m天内日销售利润少于32元的天数；
（3）如图（2）中m天内日销售面包个数在70≤x＜80这个组内的销售情况如表：
请计算该组内平均每天销售面包的个数．
（2）小明连续m天对该超市的面包销量进行统计，并制成了频数分别直方图（每个组距包含左边的数，但不包含右边的数）和扇形统计图，如图1、图2所示，请结合两图提供的信息，解答下列问题：
①m的值为30；
②求在m天内日销售利润少于32元的天数；
（3）如图（2）中m天内日销售面包个数在70≤x＜80这个组内的销售情况如表：
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
13．甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按八折收费；在乙商场累计购物，每满100元返10元．设小红在同一商场累计购物x元，其中100＜x＜300．
（1）根据题意，填写下表：
（2）当x取何值时，小红在甲、乙商场的实际花费相同？
（1）根据题意，填写下表：
| 累计购物 实际花费 | 130 | x（100＜x＜200） | 200 | x（200＜x＜300） |
| 在甲商场 | 124 | 0.8x+20 | 180 | 0.8x+20 |
| 在乙商场 | 120 | x-10 | 180 | x-20 |