题目内容
8.若关于x的不等式组$\left\{\begin{array}{l}{x-3≥a}\\{b-x≥-2}\end{array}\right.$的解集为x=2b+a+1,求使得关于x的不等式组$\left\{\begin{array}{l}{x-k≥a}\\{x+k<b}\end{array}\right.$无解的k的取值范围.分析 先求得不等式组$\left\{\begin{array}{l}{x-3≥a}\\{b-x≥-2}\end{array}\right.$的解集,根据题意求得a、b的值,即可得出不等式组$\left\{\begin{array}{l}{x-k≥0}\\{x+k<1}\end{array}\right.$,求得不等式的解集,根据题意得出k≥1-k,即可求得k的取值.
解答 解:$\left\{\begin{array}{l}{x-3≥a①}\\{b-x≥-2②}\end{array}\right.$
由①得,x≥3+a,
由②得,x≤b+2,
∵关于x的不等式组$\left\{\begin{array}{l}{x-3≥a}\\{b-x≥-2}\end{array}\right.$的解集为x=2b+a+1,
∴$\left\{\begin{array}{l}{3+a=2b+a+1}\\{b+2=2b+a+1}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$
∴$\left\{\begin{array}{l}{x-k≥0}\\{x+k<1}\end{array}\right.$,
∴解x-k≥0得,x≥k,
解x+k<1得,x<1-k,
∵关于x的不等式组$\left\{\begin{array}{l}{x-k≥a}\\{x+k<b}\end{array}\right.$无解,
∴k≥1-k,
解得k≥$\frac{1}{2}$.
点评 主要考查了一元一次不等式组的解定义,解此类题是要先用字母a,b表示出不等式组的解集,然后再根据已知解集,对应得到相等或不等关系,解关于字母a,b的方程组或不等式即可求解.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
| A. | 15元和18元 | B. | 15元和15元 | C. | 18元和15元 | D. | 18元和18元 |
 如图,已知AB=DC,BE=CF,只需再补充∠B=∠C或AB∥CD,就可以证明△ABE≌△DCF.
如图,已知AB=DC,BE=CF,只需再补充∠B=∠C或AB∥CD,就可以证明△ABE≌△DCF.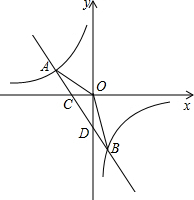 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).