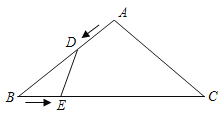
题目内容
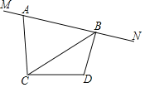
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一动点,以点
边上一动点,以点![]() 为顶点,
为顶点,![]() 为一腰作等腰
为一腰作等腰![]() ,使
,使![]() ,且
,且![]() ,设
,设![]() ,
,![]() ,我们称
,我们称![]() 为
为![]() 的“顶补三角形”.
的“顶补三角形”.
(1)求![]() 与
与![]() 的数量关系;
的数量关系;
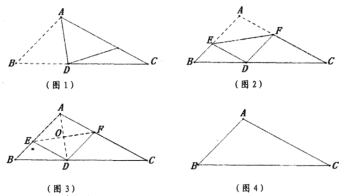
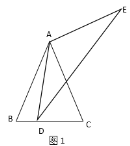
(2)如图2,![]() 为
为![]() 的“顶补三角形”,过点
的“顶补三角形”,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]() ,若四边形
,若四边形![]() 是平行四边形,求证:
是平行四边形,求证:![]() ;
;
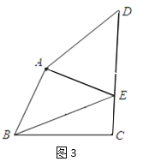
(3)如图3,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() B,
B,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据等腰三角形的内角关系可以得到![]() ,
,![]() ,再结合
,再结合![]() ,即可求出
,即可求出![]() 和
和![]() 的关系;
的关系;
(2)由于四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,则
,则![]() ,同时由
,同时由![]() 得到
得到![]() ,在(1)中得到“顶补三角形”的性质,
,在(1)中得到“顶补三角形”的性质,![]() ,所以
,所以![]() ,即可得证;
,即可得证;
(3)连接![]() ,由已知条件可以证得
,由已知条件可以证得![]() ,所以
,所以![]() ,根据三角形的外角定理可以得到
,根据三角形的外角定理可以得到![]() ,结合已知条件
,结合已知条件![]() ,可以得到
,可以得到![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() 是
是![]() 的“顶补三角形”,结合在(1)中得到“顶补三角形”的性质可以得到
的“顶补三角形”,结合在(1)中得到“顶补三角形”的性质可以得到![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() 上的高
上的高![]() ,
,![]() ,可以证得
,可以证得![]() ,相似比为
,相似比为![]() ,所以
,所以![]() ,与此同时结合等腰三角形的性质可以得
,与此同时结合等腰三角形的性质可以得![]() ,
,![]() ,所以
,所以![]() ,而
,而![]() ,所以
,所以![]() ,
,
则![]() ,即可求解;
,即可求解;
解:(1)∵在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
(2)![]() 为
为![]() 的“顶补三角形”,
的“顶补三角形”,
![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() .
.
![]() .
.
![]() .
.
![]() .
.
(3)连接![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() .
.![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,![]() ,
,
![]() 是
是![]() 的“顶补三角形”.
的“顶补三角形”.
![]() .
.
过点![]() 分别作
分别作![]() ,
,![]() 上的高
上的高![]() ,
,![]() .
.
则有![]() .
.
![]() .
.
同理可证![]() .
.
![]() .
.
![]() ,
,![]() 分别是等腰
分别是等腰![]() 与等腰
与等腰![]() 底边上的高,
底边上的高,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() .
.
![]() .
.

练习册系列答案
相关题目