ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЪЕМљ
ЮЪЬтЧщОГ
дкзлКЯгыЪЕМљПЮЩЯЃЌЭЌбЇУЧвдЁАШ§НЧаЮЕФелЕўЁБЮЊжїЬтПЊеЙЪ§бЇЛюЖЏЃЎ
ВйзїЗЂЯж
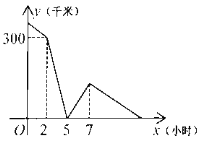
ЁАбюЛдЁБаЁзщЕФЭЌбЇгУвЛеХЖлНЧШ§НЧаЮжНЦЌ![]() ЃЌ
ЃЌ![]() ЮЊЖлНЧЃЌНјааСЫШчЯТВйзїЃК
ЮЊЖлНЧЃЌНјааСЫШчЯТВйзїЃК
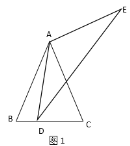
ЕквЛВНЃКШчЭМ1ЃЌелГі![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп![]() ЃЛ
ЃЛ
ЕкЖўВНЃКШчЭМ2ЃЌеЙЦНжНЦЌЃЌдйДЮелЕўИУШ§НЧаЮжНЦЌЃЌЪЙдЄЕу![]() гыЕу
гыЕу![]() жиКЯЃЌВ№Кл
жиКЯЃЌВ№Кл![]() ЗжБ№гы
ЗжБ№гы![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
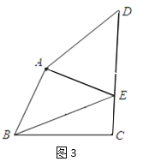
ЕкШ§ВНЃКШчЭМ3ЃЌдйДЮеЙЦНжНЦЌЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУЫФБпаЮ
ЃЌПЩЕУЫФБпаЮ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉдкЭМ4ЕФ![]() жаРћгУГпЙцзїГіелКл
жаРћгУГпЙцзїГіелКл![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈвЊЧѓЃКБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЪЕМљЬНОП
ЃЈ2ЃЉЪдХаЖЯЭМ3жаЫФБпаЮ![]() ЕФаЮзДЃЌВЂаДГіжЄУїЙ§ГЬЃЛ
ЕФаЮзДЃЌВЂаДГіжЄУїЙ§ГЬЃЛ
ЩюШыЬНОП
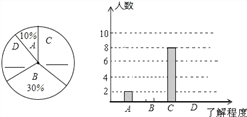
ЃЈ3ЃЉЁАГТОАШѓЁБаЁзщЕФЭЌбЇЭЛЗЂЦцЯыЃЌдкЁАбюЛдЁБаЁзщЭЌбЇВйзїЕФЛљДЁЩЯЩшМЦСЫетбљвЛИіЮЪЬтЃКдкЭМ3жаЃЌСЌНг![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌРћгУЯрЫЦШ§НЧаЮЕФжЊЪЖПЩвдЧѓГі
ЃЌРћгУЯрЫЦШ§НЧаЮЕФжЊЪЖПЩвдЧѓГі![]() ЕФГЄЃЎЧыФуаДГіЧѓНтЙ§ГЬЃЎ
ЕФГЄЃЎЧыФуаДГіЧѓНтЙ§ГЬЃЎ
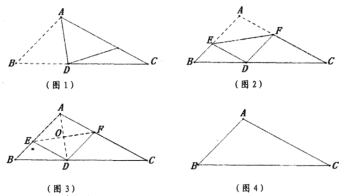
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉСтаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЌЙ§ГЬМћНтЮі
ЃЌЙ§ГЬМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉзїЁЯBACЕФНЧЦНЗжЯпADгыBCНЛгкЕуDЃЌдйзіADЕФжаДЙЯпгыABНЛгкEЃЌгыACНЛгкFМДПЩЃЛ
ЃЈ2ЃЉгЩелЕўПЩжЊЃЌ![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЌ
ЕФНЧЦНЗжЯпЃЌ![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌдйЭЈЙ§ДЙжБЦНЗжЯпКЭНЧЦНЗжЯпЕФаджЪПЩЕУ
ЕФДЙжБЦНЗжЯпЃЌдйЭЈЙ§ДЙжБЦНЗжЯпКЭНЧЦНЗжЯпЕФаджЪПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌМДПЩжЄУїЫФБпаЮ
ЃЌМДПЩжЄУїЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌдйИљОн
ЪЧЦНааЫФБпаЮЃЌдйИљОн![]() ЃЌЕУжЄЦНааЫФБпаЮ
ЃЌЕУжЄЦНааЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌЭЈЙ§жЄУї
ЃЌЭЈЙ§жЄУї![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЃЌДгЖјЕУГі
ЃЌДгЖјЕУГі![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉШчЭМЫљЪОЃЌ
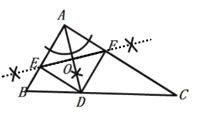
ЃЈ2ЃЉСтаЮЃЌ
жЄУїЃКгЩелЕўПЩжЊЃЌ![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЌ
ЕФНЧЦНЗжЯпЃЌ![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ
Ёп![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]()
Ёп![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп
Ёр![]()
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЁрЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌ
ЪЧЦНааЫФБпаЮЃЌ
гжЁп![]()
ЁрЦНааЫФБпаЮ![]() ЪЧСтаЮЃЎ
ЪЧСтаЮЃЎ
ЃЈ3ЃЉСЌНг![]() ЃЌ
ЃЌ
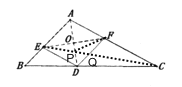
ЁпЫФБпаЮ![]() ЮЊСтаЮЃЌ
ЮЊСтаЮЃЌ
Ёр![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌ
ЃЌ
ЁрЕу![]() дк
дк![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.

 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИЁОЬтФПЁПШчЯТБэЃЌДгзѓБпЕквЛИіИёзгПЊЪМЯђгвЪ§ЃЌдкУПИіаЁИёзгжаЖМЬюШывЛИіећЪ§ЃЌЪЙЕУЦфжаЉвтШ§ИіЯрСкИёзгжаЫљЬюећЪ§жЎКЭЖМЯрЕШЃЎ
|
|
|
| 5 | 4 | ЁЁ |
ЃЈ1ЃЉПЩЧѓЕУ![]() _____ЃЛ
_____ЃЛ![]() _____ЃЛ
_____ЃЛ![]() _____ЃЎ
_____ЃЎ
ЃЈ2ЃЉЕк2019ИіИёзгжаЕФЪ§ЮЊ______ЃЛ
ЃЈ3ЃЉЧА2020ИіИёзгжаЫљЬюећЪ§жЎКЭЮЊ______ЃЎ
ЃЈ4ЃЉЧА![]() ИіИёзгжаЫљЬюећЪ§жЎКЭЪЧЗёПЩФмЮЊ2020ЃПШєФмЃЌЧѓГі
ИіИёзгжаЫљЬюећЪ§жЎКЭЪЧЗёПЩФмЮЊ2020ЃПШєФмЃЌЧѓГі![]() ЕФжЕЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ