Question

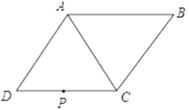
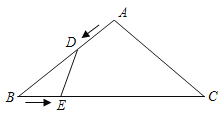
【题目】如图所示，在等腰△ABC中，AB＝AC＝10cm，BC＝16cm．点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s．连接DE，设运动时间为t（s）（0＜t＜10），解答下列问题：

（1）当t为何值时，△BDE的面积为7.5cm2；

（2）在点D，E的运动中，是否存在时间t，使得△BDE与△ABC相似？若存在，请求出对应的时间t；若不存在，请说明理由．

Answer 1

【答案】（1）t为5秒时，△BDE的面积为7.5cm2；（2）存在时间t为或秒时，使得△BDE与△ABC相似．

【解析】

（1）根据等腰三角形的性质和相似三角形的判定和性质求三角形BDE边BE的高即可求解；

（2）根据等腰三角形和相似三角形的判定和性质分两种情况说明即可．

解：（1）分别过点D、A作DF⊥BC、AG⊥BC，垂足为F、G

如图

∴DF∥AG，＝

∵AB＝AC＝10，BC＝16∴BG＝8，∴AG＝6．

∵AD＝BE＝t，∴BD＝10﹣t，

∴＝

解得DF＝（10﹣t）

∵S△BDE＝BEDF＝7.5

∴（10﹣t）t＝15

解得t＝5．

答：t为5秒时，△BDE的面积为7.5cm2．

（2）存在．理由如下：

①当BE＝DE时，△BDE与△BCA，

∴＝即＝，

解得t＝，

②当BD＝DE时，△BDE与△BAC，

＝即＝，

解得t＝．

答：存在时间t为或秒时，使得△BDE与△ABC相似．